Trong bài viết trước chúng ta đã tìm hiểu về cách tối thiểu hoá hàm số, từ đó áp dụng vào tối thiểu hoá cost function J(θ). Hôm nay chúng ta sẽ đi vào tìm hiểu về giải thuật “Gradient descent” nhằm khắc phục nhược điểm của phương pháp tìm nghiệm của J’(θ) = 0 (đạo hàm của J(θ)) và giới thiệu về mô hình “Linear Regression” (Hồi quy tuyến tính).

1. Gradient descent:

Chúng ta đã biết đạo hàm của hàm số là hàm số mô tả sự biến thiên của slope trên từng điểm của hàm số đó. Bên cạnh đó slope tại một điểm trên hàm số hay đạo hàm tại điểm đó của hàm số cho ta biết hàm số đang tăng, giảm hay đạt cực đại, cực tiểu.

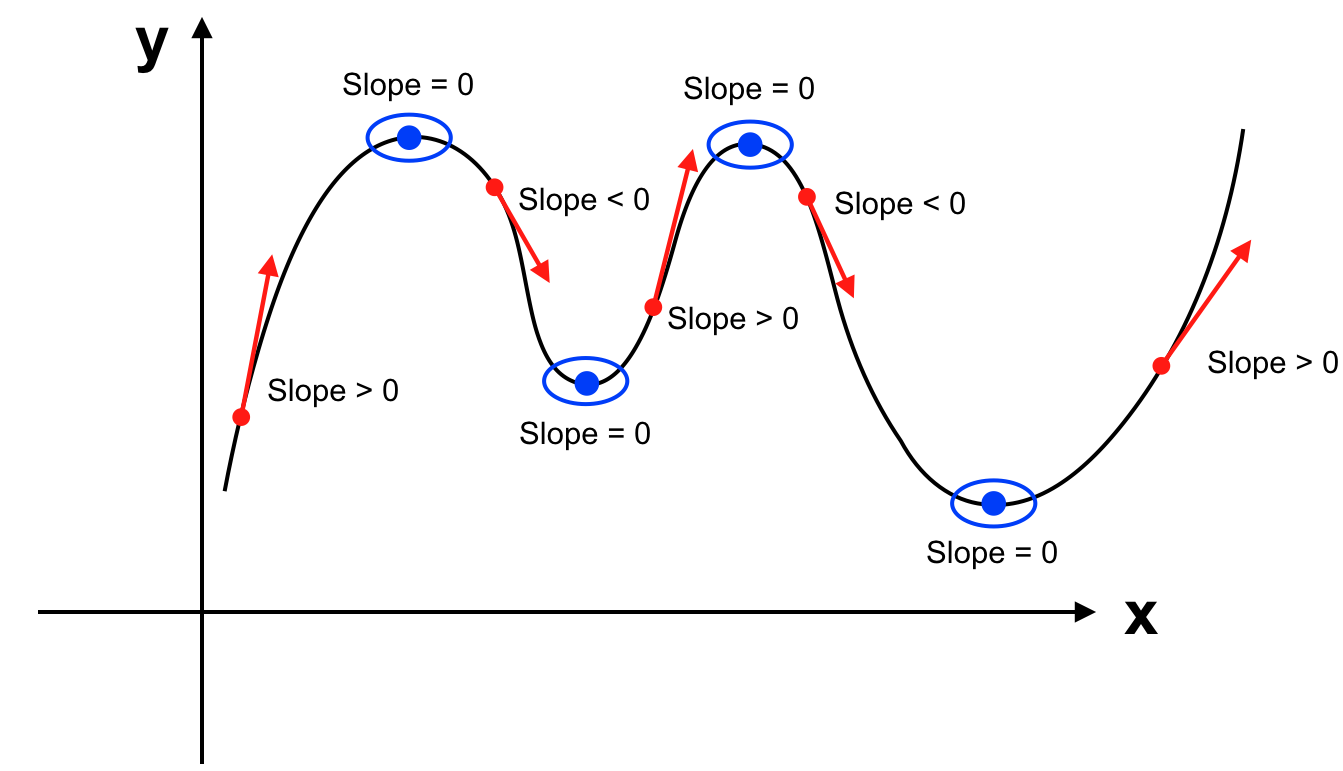
Phương pháp thông thường trong toán học là ta giải phương trình J’(θ) = 0. Tuy nhiên phương trình không phải lúc nào cũng dễ giải và chi phí để giải phương trình khi số lượng biến lớn cũng khiến performance của hệ thống bị ảnh hưởng.

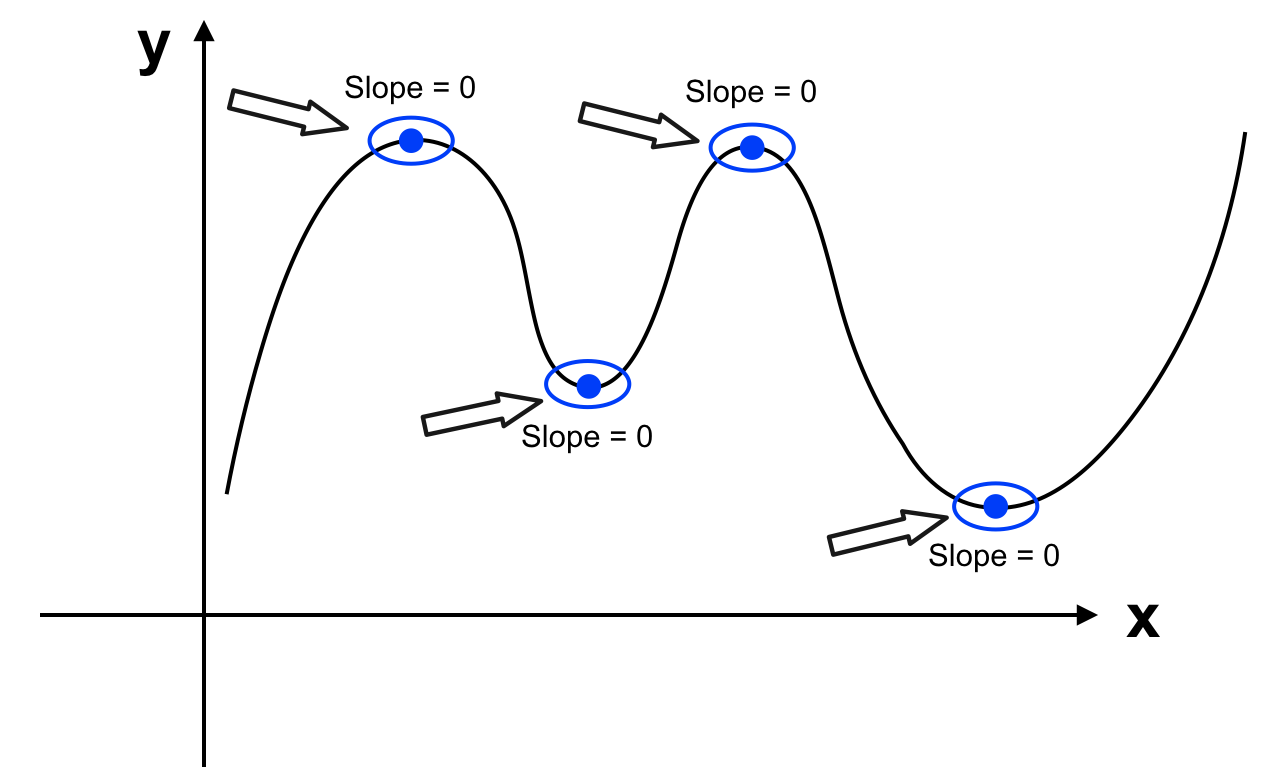
Vấn để được đặt ra là nếu không giải phương trình, với giá trị θ hiện tại (chẳng hạn ban đầu tất cả tham số θ = 0) làm sao để thay đổi θ để cho J(θ) nhỏ hơn (chưa phải nhỏ nhất), nếu như lặp lại quá trình này nhiều lần thì ta sẽ chọn được θ sao cho J(θ) gần với giá trị nhỏ nhất của J(θ) hay điểm cực tiểu của hàm số. Giả sử với θ hiện tại, giá trị của J(θ) như hình sau:

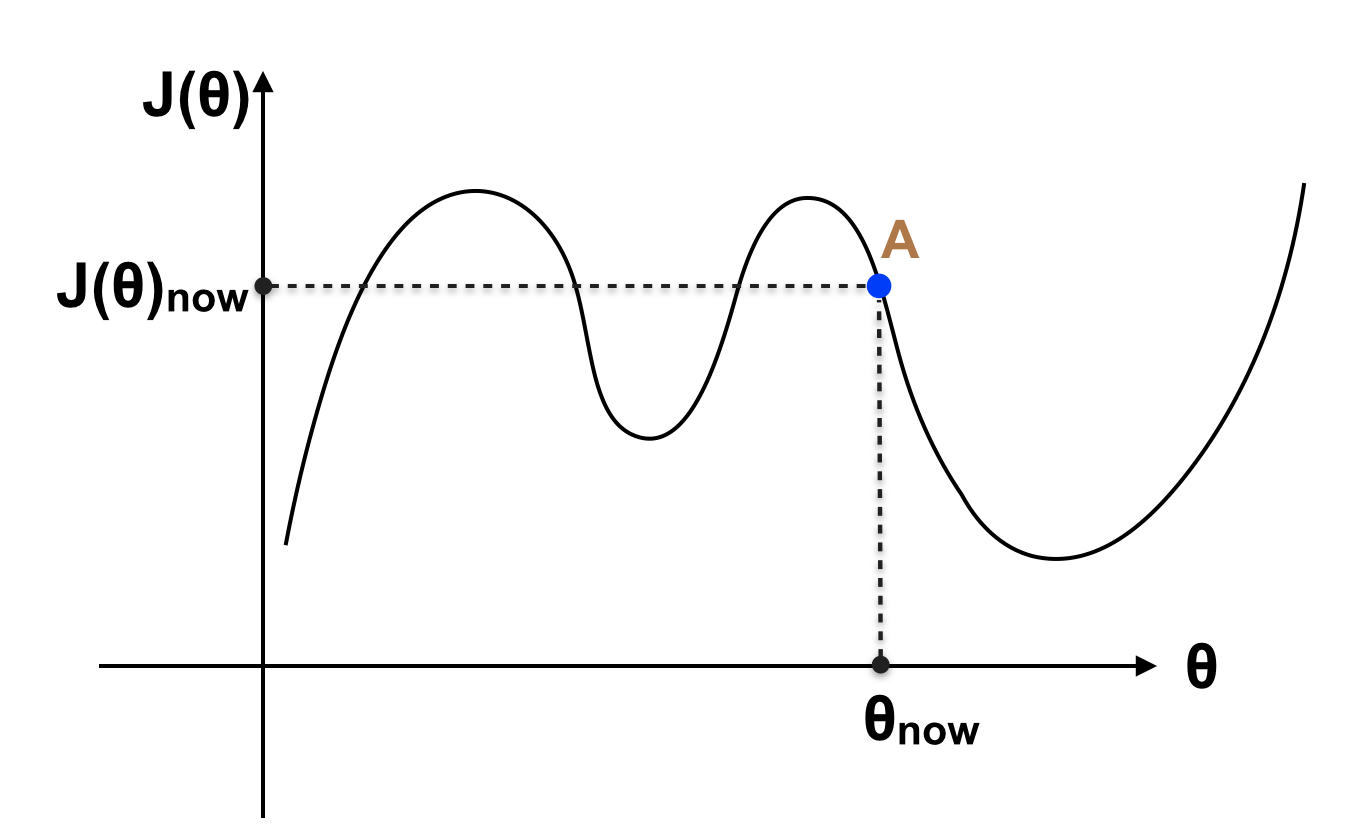
Với θ hiện tại, J(θ) đang ở điểm A, rõ ràng ở vị trí A đồ thị trên đang có xu hướng giảm (đạo hàm hay slope tại điểm A < 0, nếu tăng θ thì J(θ) sẽ giảm). Ta tăng θ để A tiến đến điểm B như hình sau:

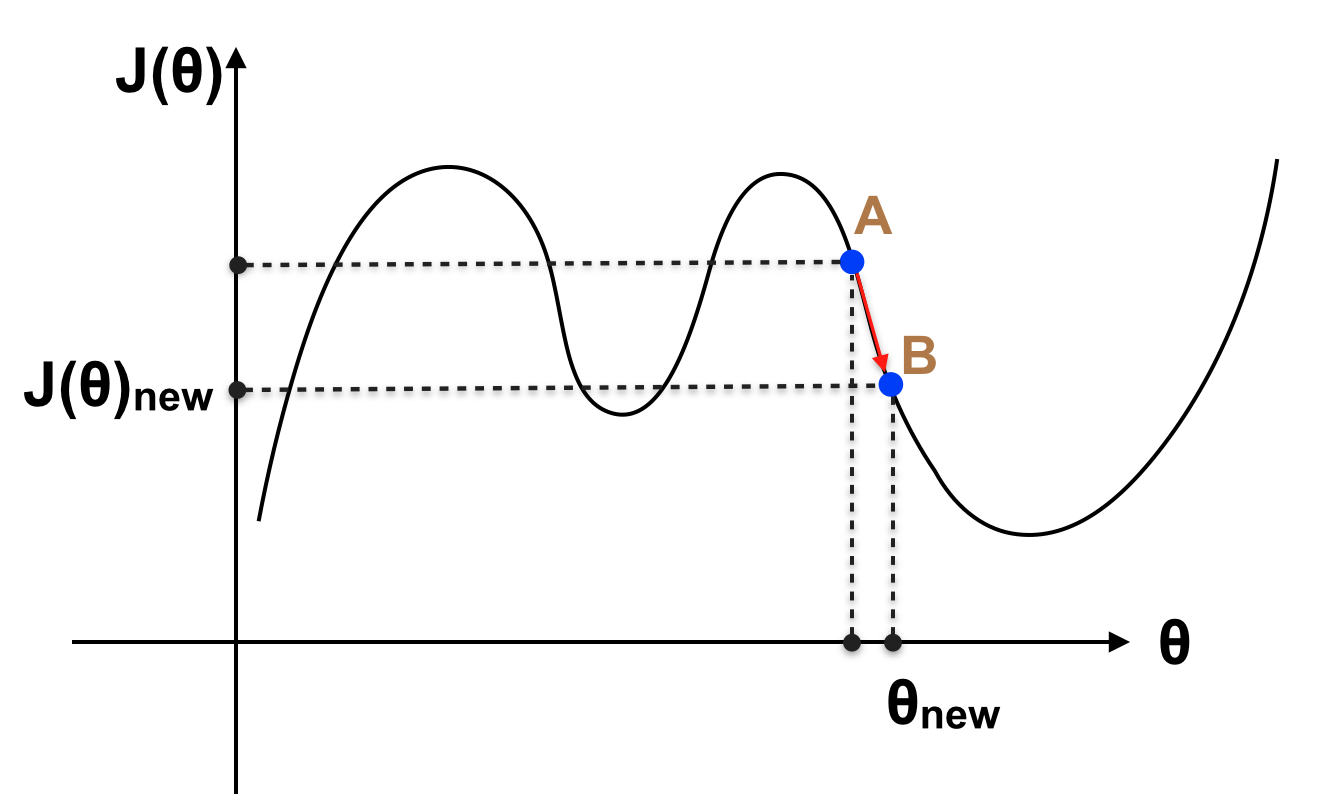
Khi đó J(θ) giảm xuống (vì slope tại A < 0 thì khi tăng θ thì J(θ) sẽ giảm. Vậy với giá trị θ hiện tại, chúng ta đã biết tăng hay giảm θ để giá trị của J(θ) giảm xuống. Thử tưởng tượng rằng chúng ta làm việc này một cơ số lần, khi đó J(θ) sẽ giảm dần xuống giá trị cực tiểu gần nhất (cực tiểu địa phương – Local minimum).

Giải thuật được mô tả như sau:
  • Khởi tạo θ bất kì (thường tất cả tham số θ được gán = 0).
  • Liên tiếp thay đổi θ := θ – α * J’(θ) đồng thời (tất cả các tham số θ phải được thay đổi cùng 1 lúc)
  • Dừng lại khi J(θ) có thay đổi không đáng kể. Trong đó α được gọi là Learning rate (dùng để điều chỉnh tốc độ học của máy). Trước khi đi vào giải thích về tham số này, chúng ta nói một chút về nhược điểm của giải thuật này.

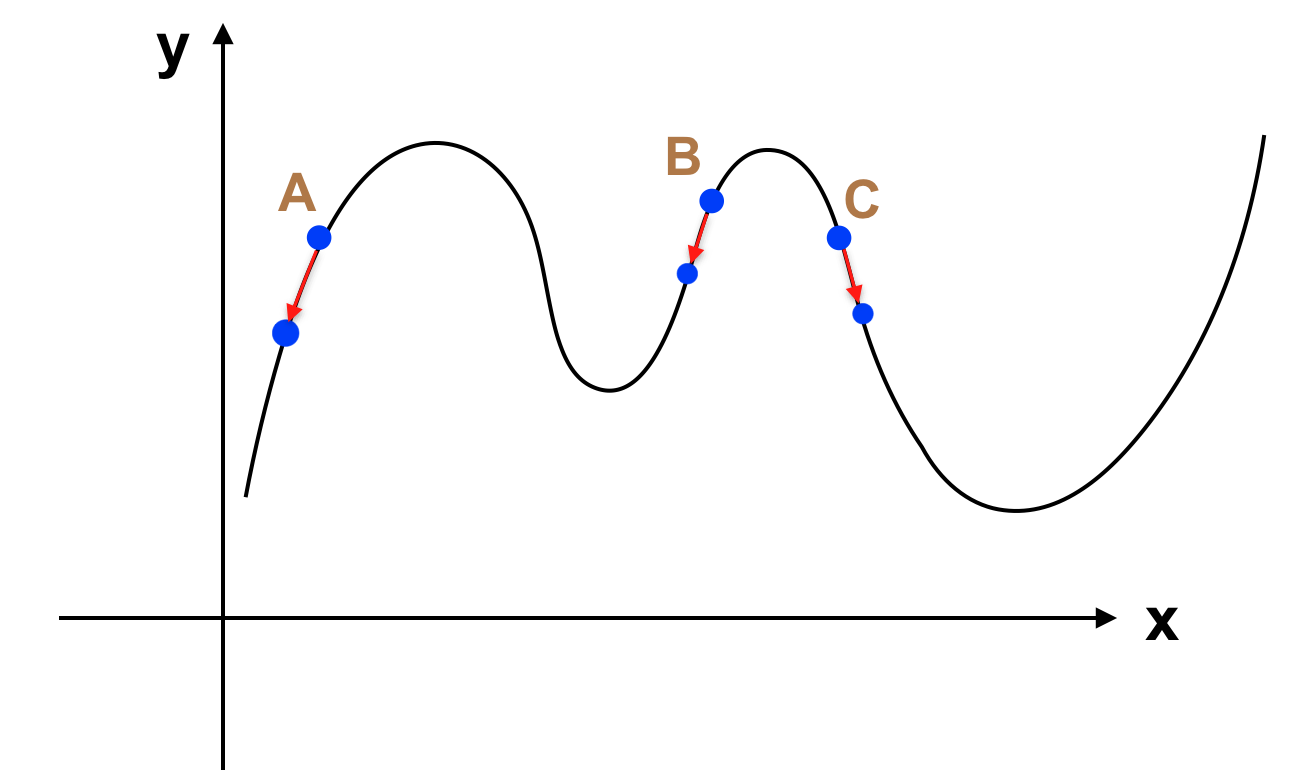
  • Khi ta đang ở điểm A, có thể giải thuật này sẽ đi vào vòng lặp vô hạn do hàm số đi xuống mãi khi giảm θ. Tuy nhiên trong trường hợp này việc giải phương trình cũng không mang lại kết quả do bản thân hàm số J(θ) không có giá trị nhỏ nhất (Global minimum). Cách giải quyết là ta phải xây dựng hàm J(θ) có giá trị nhỏ nhất. Chẳng hạn:

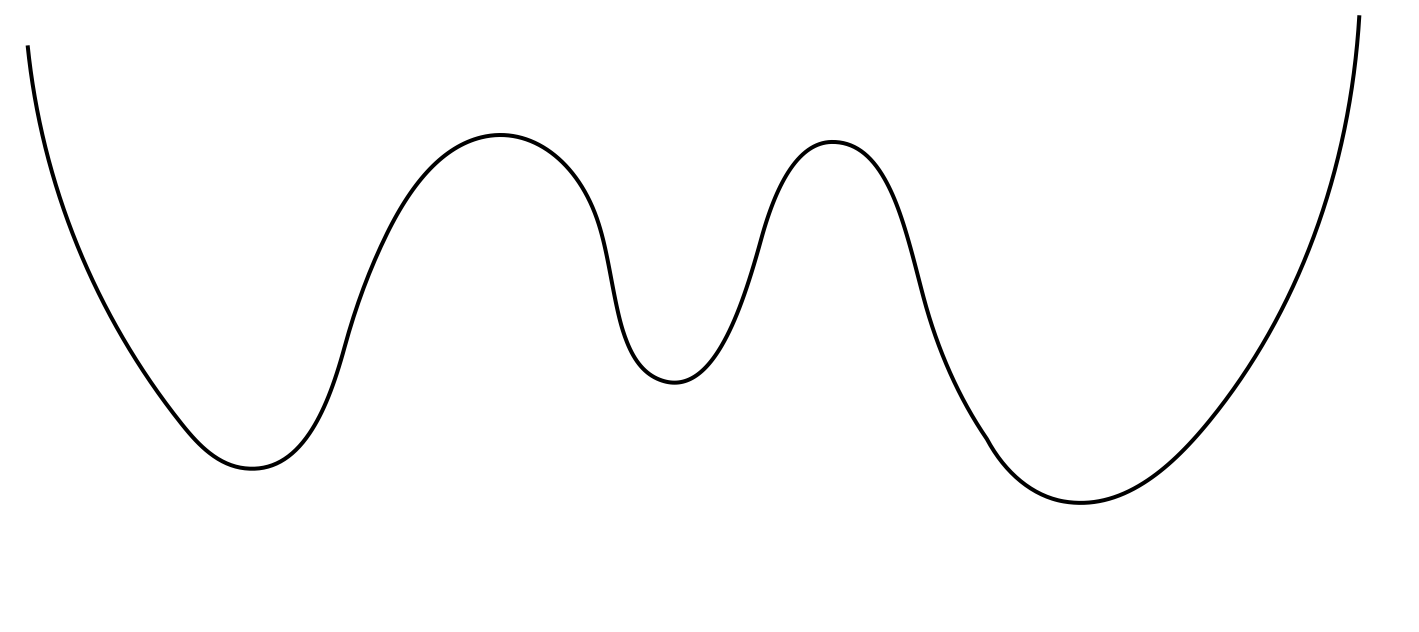
  • Khi ta đang ở điểm B và điểm C, áp dụng giải thuật trên sẽ đưa ta đến 2 điểm cực tiểu khác nhau. Rõ ràng tại C, ta sẽ giảm được J(θ) nhiều hơn, chính vì thế để đảm bảo J(θ) đạt được giá trị nhỏ nhất, ta phải cố gắng xây dựng J(θ) có dạng tương tự như parabolla. Khi đó J(θ) sẽ chỉ có một giá trị nhỏ nhất, và giải thuật chắc chắn đưa J(θ) xuống đáy của đồ thị.

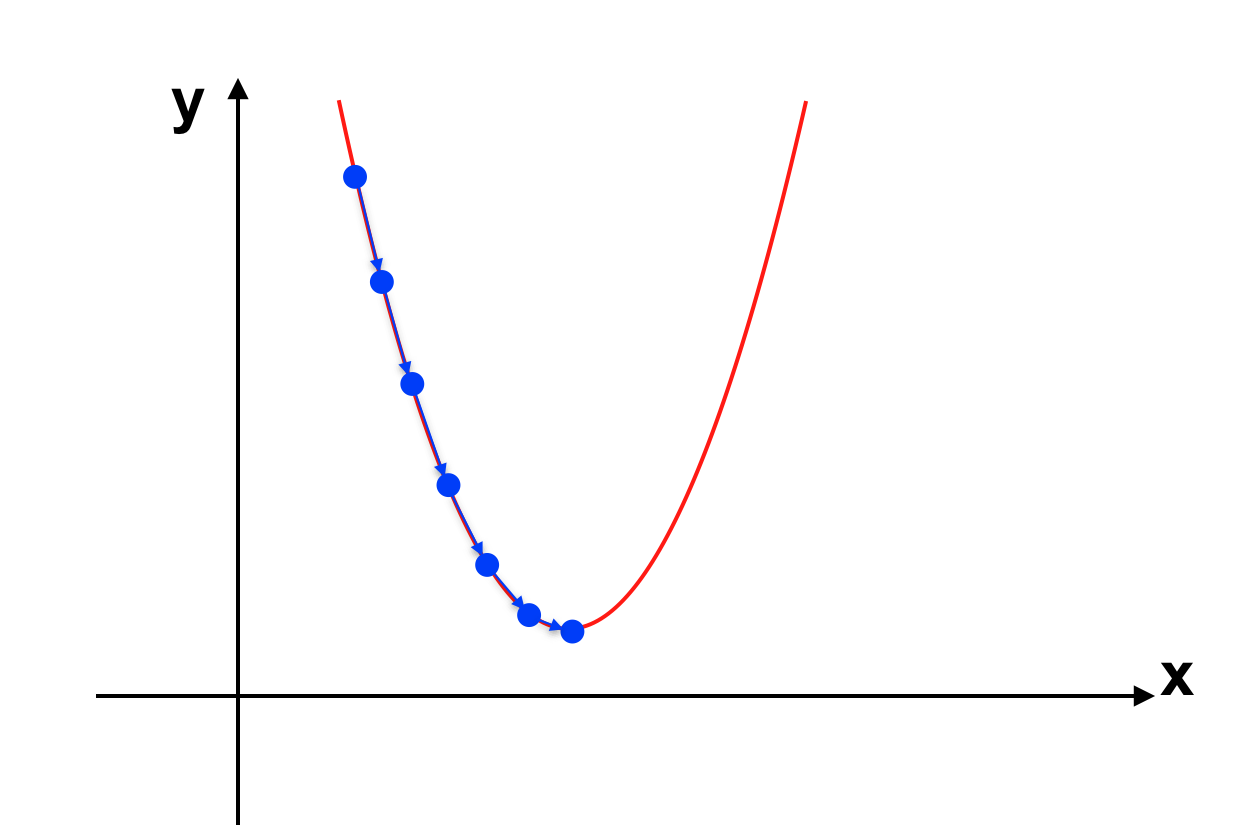
Trở lại với vấn đề về Learning rate α. Nếu như ta loại bỏ tham số α thì chẳng qua là để α = 1 (giải thuật trở thành θ := θ – J’(θ)). Việc xác định được các tham số θ nhanh hay chậm phụ thuộc vào tham số này, tuy nhiên nếu như lựa chọn không phù hợp có thể gây ra hệ luỵ nhất định. Cụ thể như sau:

  • α quá nhỏ: α nhỏ sẽ khiến cho các bước đi xuống dốc của J(θ) cũng nhỏ => việc học mất nhiều thời gian hơn.
  • α quá lớn: α lớn sẽ khiến cho các bước đi trở nên quá lớn, có thể khiến J(θ) lớn hơn giá trị hiện tại. Như hình vẽ sau:

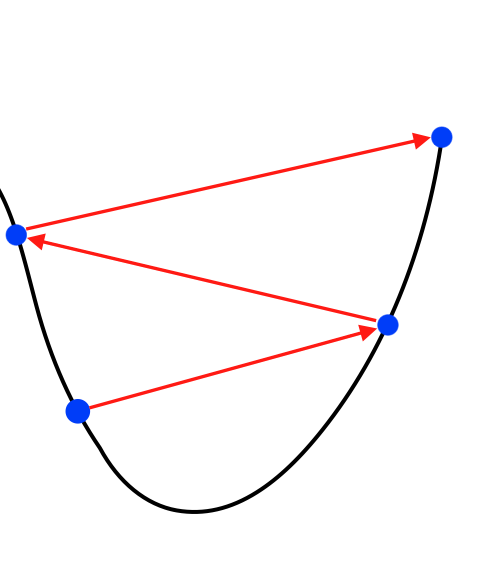
2. Linear Regression:

Bây giờ chúng ta sẽ đến với một mô hình cụ thể. Đặc biệt đây là mô hình đơn giản nhất trong ML, mô hình “Hồi quy tuyến tính” (Linear Regression). Bài toán: Ta có một tập dữ liệu để máy học như sau:

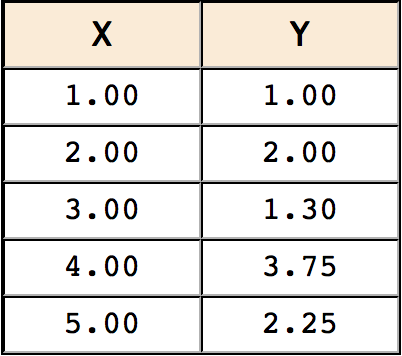
Vì là ví dụ nên lượng dữ liệu nhỏ, trên thực tế, chúng ta cần một lượng lớn dữ liệu để có thể xây dựng mô hình chính xác hơn. Ta đưa dữ liệu trên vào đồ thị như sau:

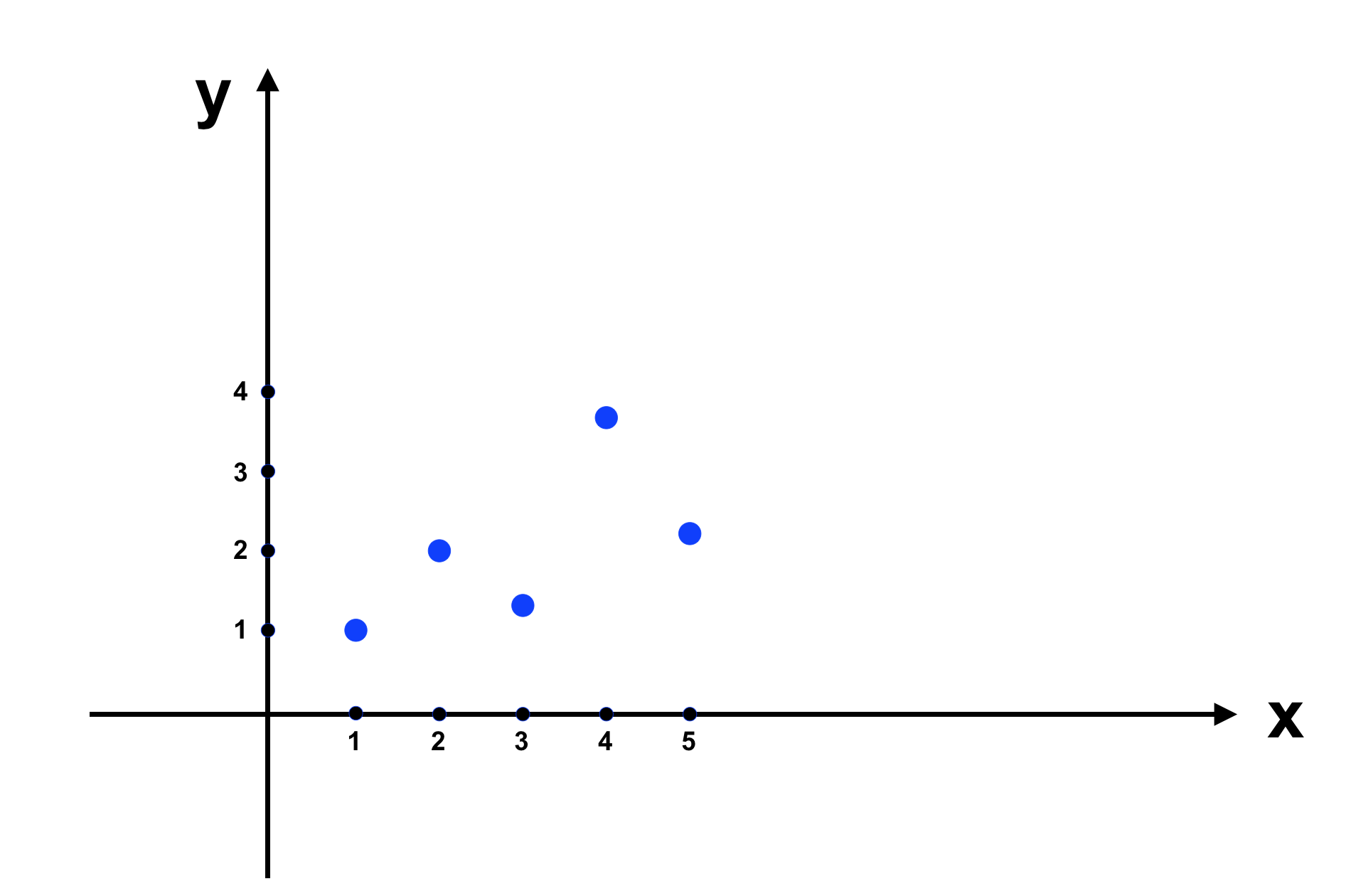
Bây giờ chúng ta xây dựng một hàm số có dạng đồ thị là đường thẳng, và cố gắng khiến nó gần giống với f(x) nhất. Nhắc lại rằng hàm số có đồ thị là đường thằng có dạng như sau: y = \(θ_1x + θ_0\) trong đó x là input và y là output. Trong hình vẽ trên, những điểm được vẽ bởi tập dữ liệu học chính là những điểm nằm trên đồ thị hàm số f(x). Chúng ta bắt đầu với đường thẳng \(h(x) = x + 1\) (trong trường hợp này \(θ_1 = 1\) và \(θ_0 = 1\) là các tham số θ chúng ta vẫn nhắc tới từ trước đến giờ).

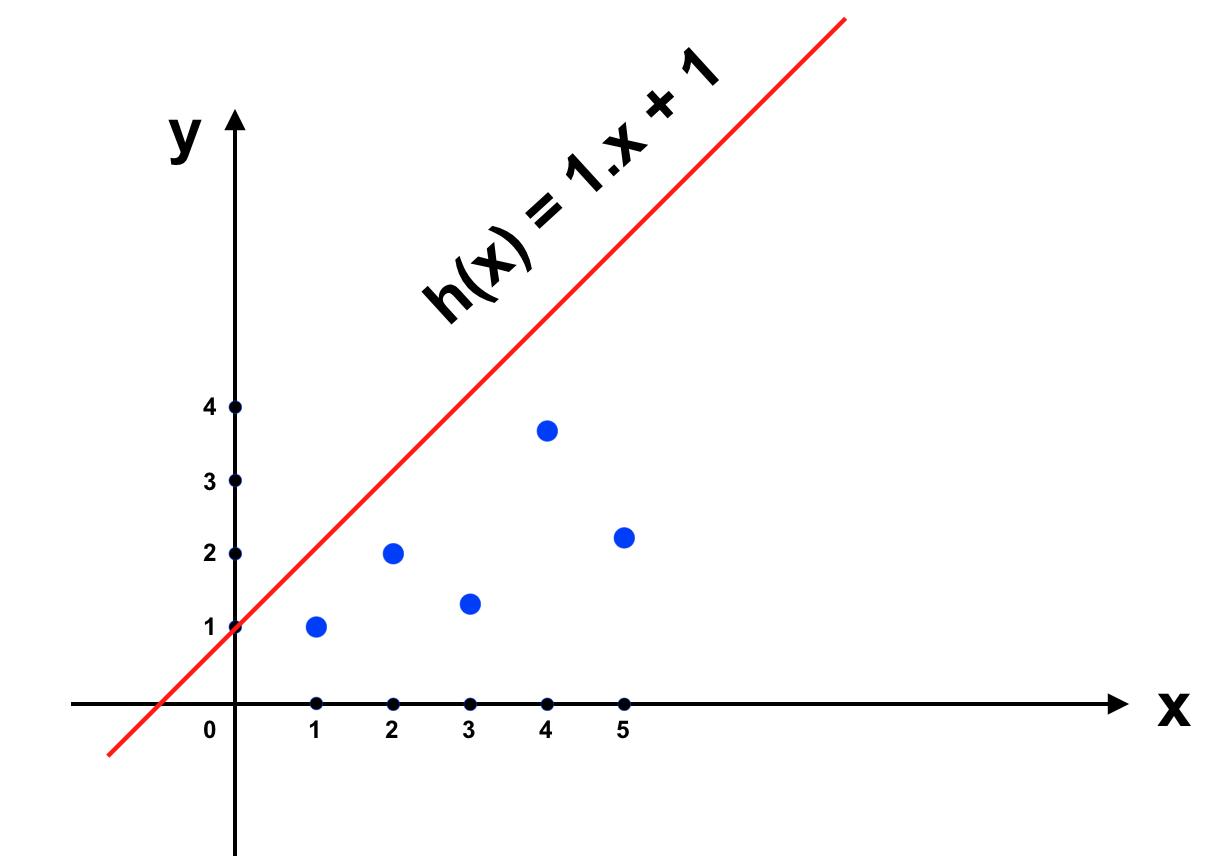
Ta thấy rằng khi đó J(θ) sẽ là hàm số 2 biến \(θ_1\) và \(θ_0\), khi đó để mô tả J(θ) trên đồ thị chúng ta sẽ cần tới đồ thị 3 chiều (\(θ_1\), \(θ_0\) và J(θ)). Để đơn giản và có thể trình bày trực tiếp trên đồ thị 2 chiều, tôi sẽ bỏ bớt 1 tham số \(θ_0\) hay mặc định cho \(θ_0 = 0\) tương đương với việc để J(θ) đi qua gốc toạ độ \((0, 0)\). Đồ thị của chúng ta sẽ trở thành như sau:

Với h(x) như trên thì khi \(x = 3\) => \(h(x) = 3\), có vẻ không được chính xác lắm. Ta sẽ thay đổi \(θ_1 = 1\) để h(x) dự đoán được kết quả gần với \(y = f(x)\) hơn. Sai số của h(x) và f(x) đơn giản nhất là \(J = h(x) – f(x)\) => \(J(θ) = ∑[h(x) – f(x)] = ∑[h(x) – y]\) (được tính trên tất cả dữ liệu chúng ta có cho máy học). Cụ thể trong ví dụ này: \(J(θ) = [h(1) – 1] + [h(2) – 2] + [h(3) – 1.3] + [h(4) – 3.75] + [h(5) – 2.25]\)

Tuy nhiên \(h(x) – f(x)\) tuỳ trường hợp sẽ có giá trị âm hoặc dương nên chúng không thể hiện được sự sai khác giữa h(x) và f(x). Nếu lấy giá trị tuyệt đối \(|h(x) – f(x)|\) sẽ khiến cho J(θ) trở nên phức tạp, nên để khắc phục ta bình phương chúng (phương pháp này còn gọi là Least Square – tối thiểu hoá phần diện tích hình vuông có cạnh là sự sai khác giữa giá trị dự đoán và giá trị thực tế). 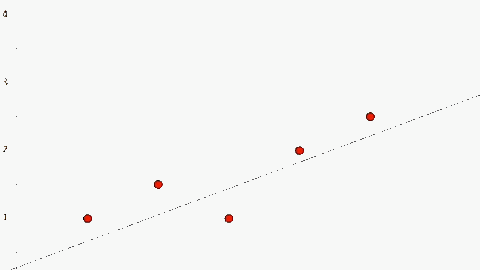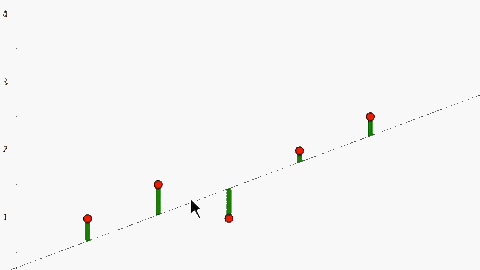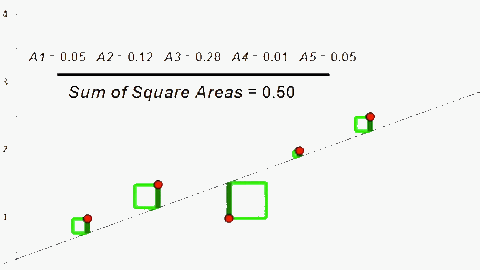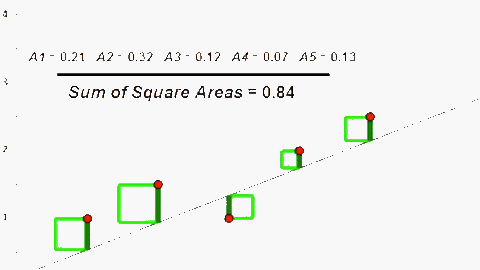\(=> J(θ) = ∑[h(x) – f(x)]^2 = [h(1) – 1]^2 + [h(2) – 2]^2 + [h(3) – 1.3]^2 + [h(4) – 3.75]^2 + [h(5) – 2.25]^2 = 10.515\) Giờ chúng ta sẽ làm cho J(θ) nhỏ đi, để nguyên tham số \(θ_1\) ta có \(J(θ) = ∑[θ_1x – y]^2\). Hàm số J(θ) là hàm bậc 2, đồ thị có dạng parabolla (đúng như trong giải thuật Gradient descent mong muốn). Trước tiên ta sẽ sử dụng phương pháp Normal Equation để tìm J(θ) nhỏ nhất.

\[\begin{align*} & J(θ) \\ & = ∑(θ_1x - y)^2 \\ & = ∑(θ_1^2x^2 - 2θ_1xy + y^2)\\ & = ∑θ_1^2x^2 - ∑2θ_1xy + ∑y^2\\ & = θ_1^2(∑x^2) - θ_1(∑2xy) + ∑y^2\\ & => J'(θ) = 2θ_1(∑x^2) - (2∑xy)\\ \end{align*}\]

Suy ra:

\[\begin{align*} & J'(θ) = 0 \\ & <=> 2θ_1(∑x^2) - (2∑xy) = 0 \\ & <=> θ_1 = \frac{2∑xy}{2∑x^2} = \frac{∑xy}{∑x^2} \\ \end{align*}\]

Nhưng vì số lượng dữ liệu đưa vào có thể thay đổi (chẳng hạn khi ta đưa thêm dữ liệu vào cho máy học) nên \(J(θ) = \frac{1}{m}∑[h(x) – f(x)]^2\) sẽ tổng quát hơn. Bên cạnh đó vì J(θ) là hàm số bậc 2 nên khi đạo hàm ta sẽ thu được hàm số có dạng \(2g(x)\) (vì \(f(x) = x^2\) thì \(f’(x) = 2x)\), nên để cho gọn ta thêm \(\frac{1}{2}\) vào \(J(θ) => J(θ) = \frac{1}{2m} ∑[h(x) – f(x)]^2\) Trong ví dụ trên sau khi giải phương trình ta có : \(θ = \frac{45.15}{55} \approx 0.82\) . Đưa vào đồ thị ta có:

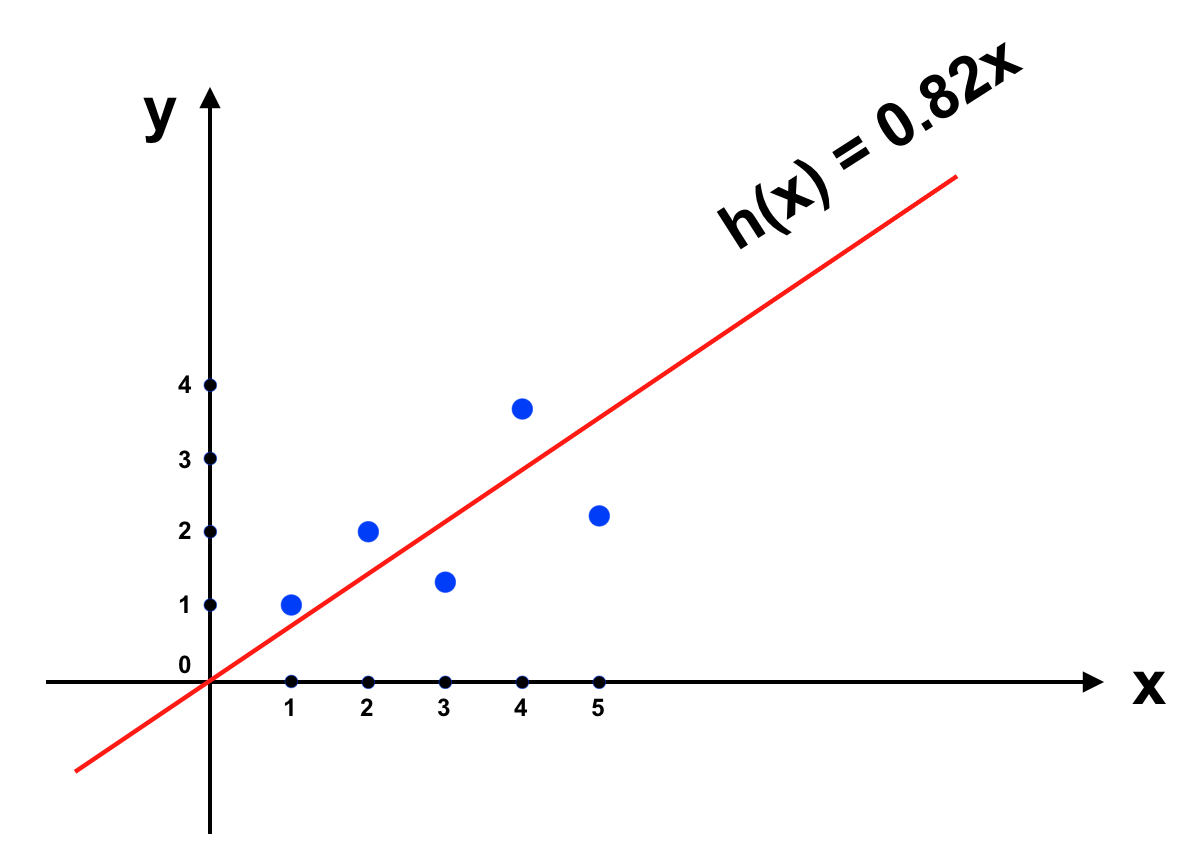
Trông có vẻ ổn, các bạn hãy thử áp dụng giải thuật Gradient descent với ví dụ này xem có thu được kết quả tương tự không nhé. Để ví dụ đơn giản nên tôi chỉ đưa ra mô hình “Linear Regression” trong trường hợp có 1 tham số θ. Với h(x) không nhất thiết đi qua gốc toạ độ chúng ta sẽ có thêm tham số \(θ_0\), khi đó J(θ) sẽ không dừng lại ở dạng parabolla mà sẽ là hàm số 2 biến phải được mô tả trong không gian 3 chiều và đồ thị của nó có dạng như sau:

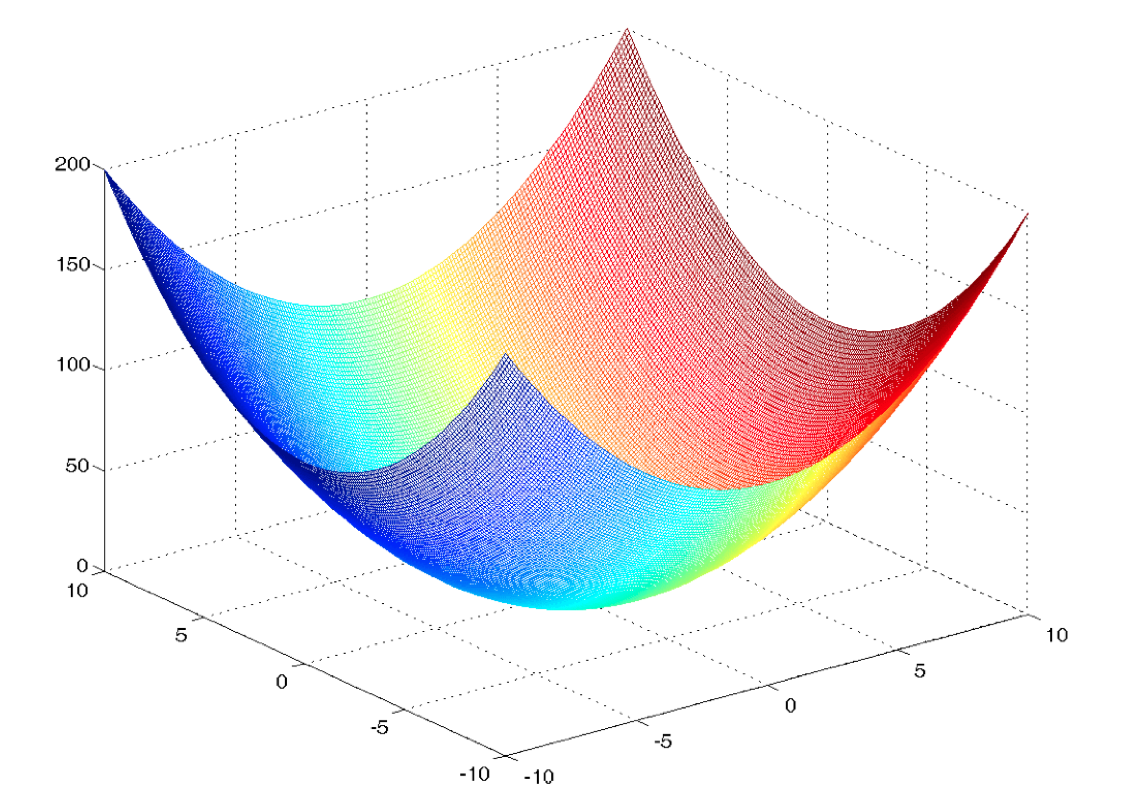
Đối với không gian \(\mathbf{n}\) chiều, \(\mathbf{x}\) không chỉ là một giá trị vô hướng mà là một vector với toạ độ trên n trục. Ta có mô hình Linear Regression tổng quát như sau:

  • Tập dữ liệu với \(\mathbf{m}\) cặp dữ liệu:

\(x = (x_1, x_2, …, x_n)\)

\(y = f(x)\)

  • Hàm tiên đoán hypothesys:

\(h(x) = θ_0 + θ_1x_1 + … + θ_n x_n = ∑ θ_i x_i\) (trong đó \(x_0 = 1)\)

  • Cost function:

\(J(θ) = \frac{1}{2m} * ∑[h(x) – y]^2 = \frac{1}{2m} * ∑[∑ θ_i x_i – y]^2\)

\(J’(θ) = \frac{1}{m} ∑[(∑ θ_i x_i – y)x]\)

Trong đó

\(J’(θ_j) = \frac{1}{m} ∑[(∑ θ_i x_i – y)x_j]\) (\(x_j\) là giá trị \(\mathbf{x}\) tương ứng trong \(θ_j x_j\))

Đến đây hi vọng các bạn đã nắm được giải thuật Gradient descent và quá trình học trên một mô hình của ML như thế nào. Hẹn gặp lại các bạn trong bài viết sau.