[ML – 04] From Linear Regression model to Polynomial Regression model
Chào các bạn, trong bài viết trước chúng ta đã tìm hiểu về mô hình Linear Regression với ví dụ đơn giản nhất trên không gian 2 chiều cho \(\mathbf{h(x)}\). Trong bài viết này chúng ta sẽ phát triển mô hình Linear Regression (hồi quy tuyến tính) lên mô hình tổng quát hơn “Polynomial Regression” (hồi quy đa thức). Trước tiên, chúng ta sẽ tổng kết lại về Linear Regression:
1. Nhắc lại về mô hình Linear Regression:
Mô hình hồi quy tuyến tính sử dụng hàm số tuyến tính (được biểu diễn dưới dạng một đường thẳng trên đồ thị) làm hàm tiên đoán \(\mathbf{h(x)}\)
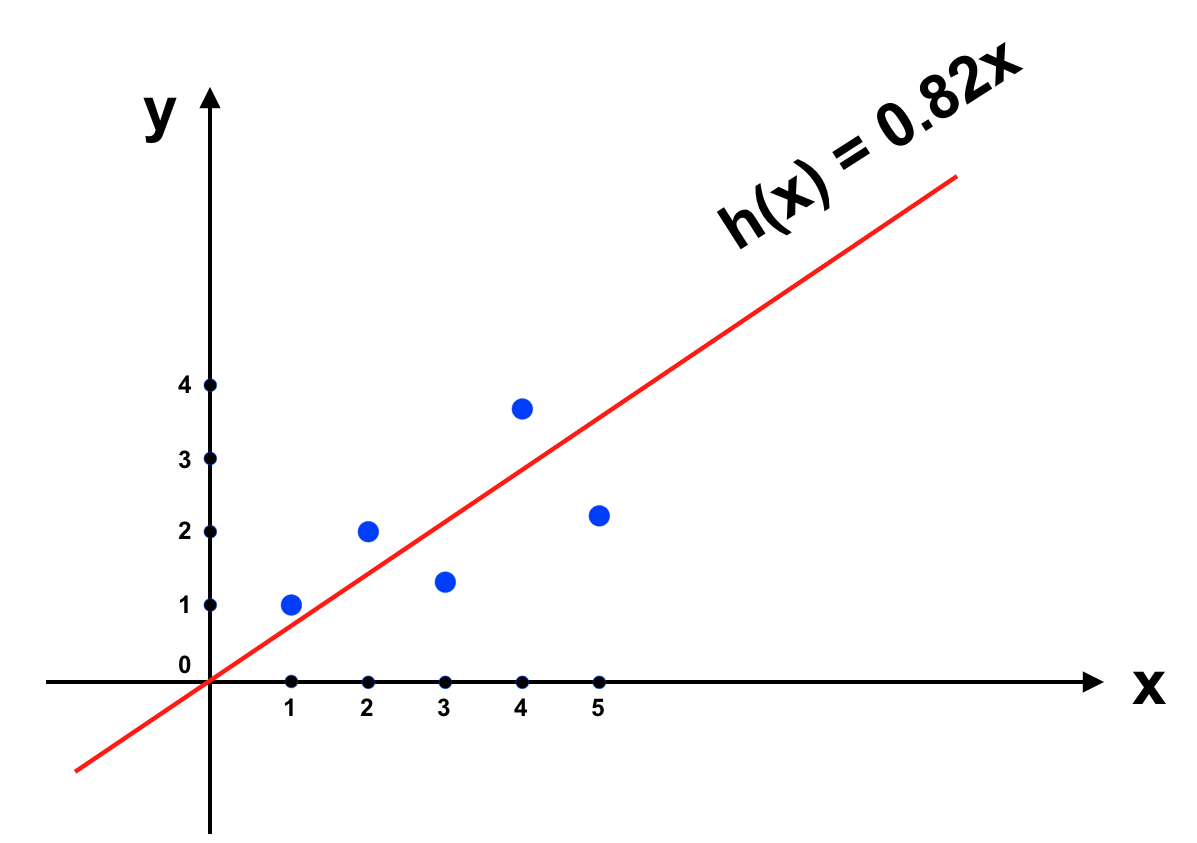
Sai số của \(\mathbf{h(x)}\) được tính toán dựa trên bình phương sai khác giữa \(\mathbf{h(x)}\) và \(\mathbf{y}\) thực tế. Do đó để tối thiểu sai số của \(\mathbf{h(x)}\) ta sử dụng phương pháp (hay giải thuật) Least Mean Square (LMS).
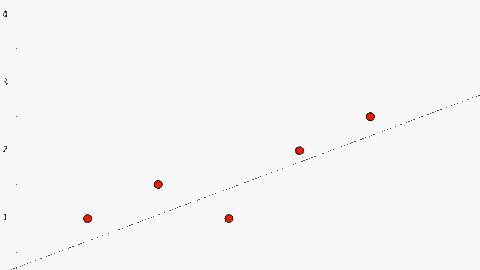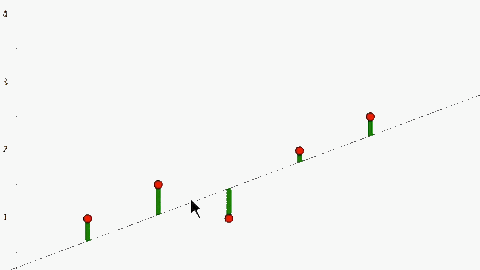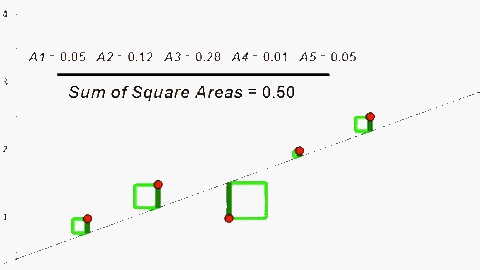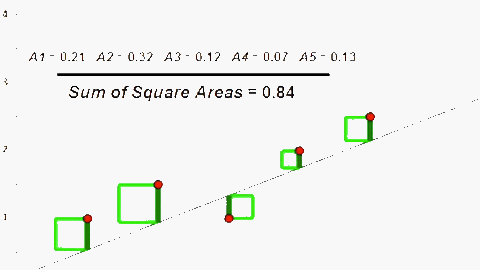
\[J(\theta) = \frac{1}{2m}\sum_{i=1}^m(h_{\theta}(x^{(i)}) - y^{(i)})^2\]
Tối thiểu \(\mathbf{J(θ)}\) để thu được hàm số dự đoán tốt nhất trong mô hình hồi quy tuyến tính bằng các giải phương trình \(\mathbf{J’(θ)} = 0 \). Với hàm số \(\mathbf{J(θ)}\) được xây dựng như trên chỉ là hàm bậc 2 nên đạo hàm của nó chỉ là hàm bậc 1 nên phương trình có nghiệm duy nhất. Một phương pháp khác là giảm dần giá trị θ theo độ dốc của hàm số (giải thuật Gradient Descent). Dạng của \(\mathbf{J’(θ)}\) như sau:
\[\\ \begin{align*} \frac{\partial}{\partial \theta _j} & = \frac{\partial}{\partial \theta _j} \frac{1}{2} (h_{\theta}(x) - y)^2) \\ & = 2 . \frac{1}{2}(h_{\theta}(x) - y) . \frac{\partial}{\partial \theta_j}(h_{\theta}(x) - y) \\ & = (h_{\theta}(x) - y)\frac{\partial}{\partial \theta_j}(\sum_{i=0}^n{\theta _i}x_i - y)\\ & = (h_{\theta}(x) - y)x_j \end{align*}\]Trong đó \(θ_j\) là giá trị tại hàng \(j\) của vector \(\theta\).
\(x_j\) trong \(h(\theta) = \sum\theta_jx_j (x_0 = 1)\).
Với giải thuật Gradient Descent giá trị của \(J(\theta)\) sẽ giảm dần về điểm cực tiểu như sau:
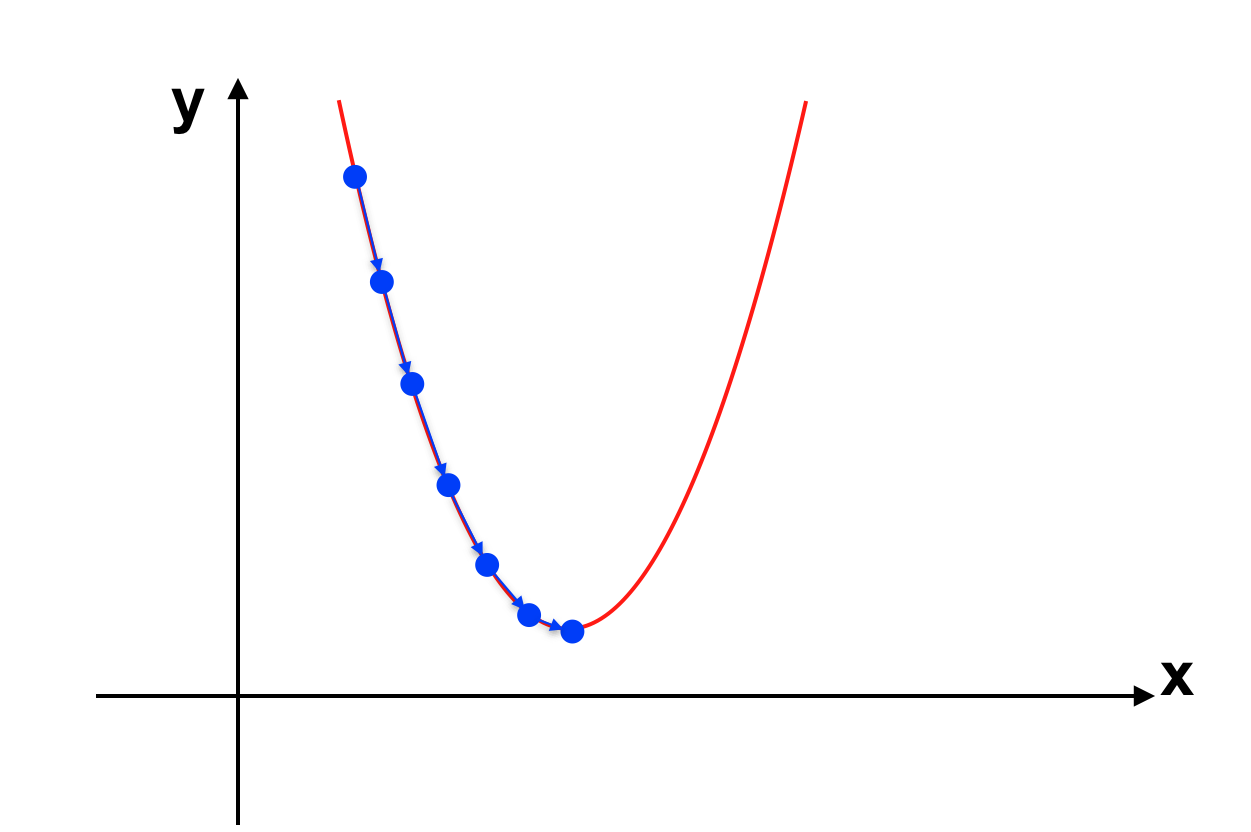
2. Phát triển Linear Regression thành Polynomial Regression:
Ta áp dụng mô hình Linear Regression trong trường hợp sau:
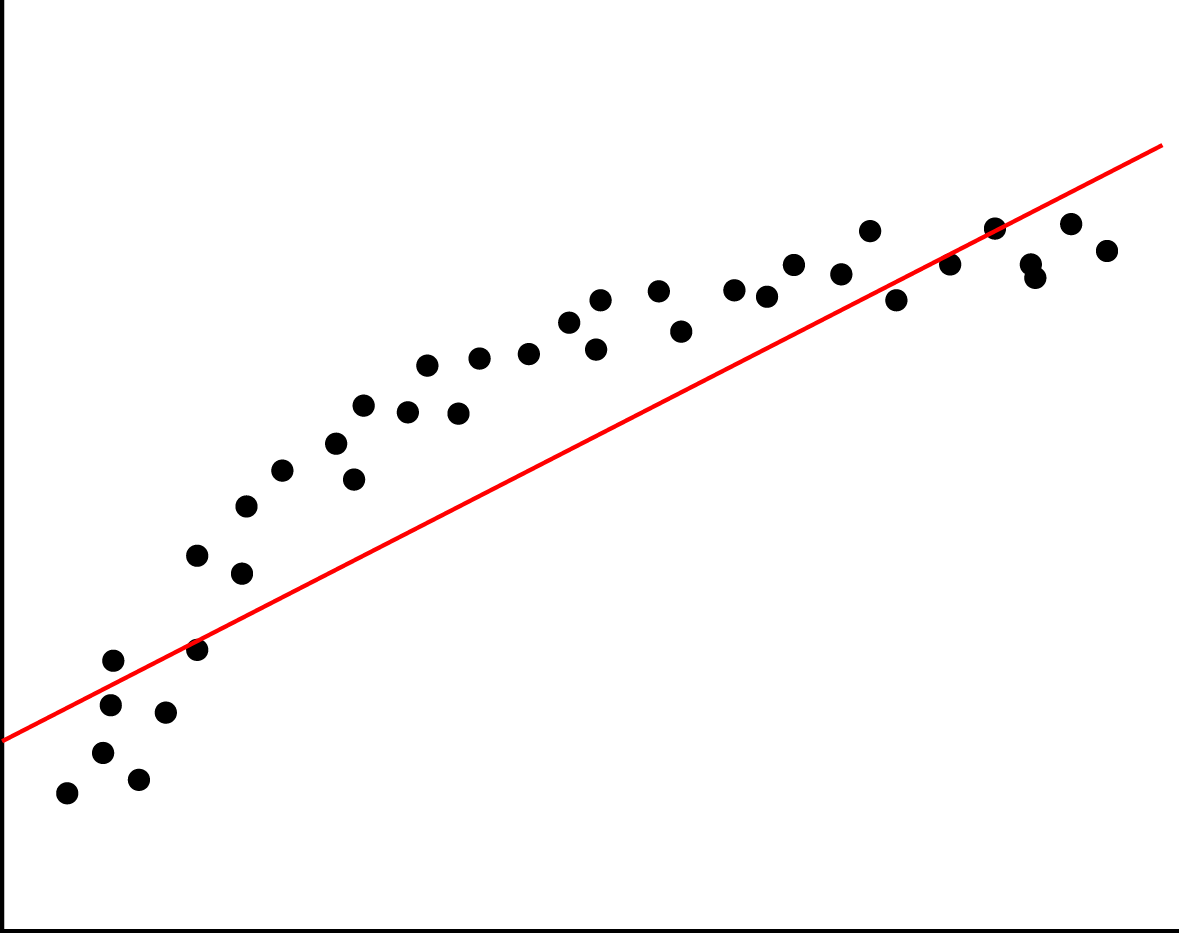
Trong trường hợp này ta thấy có vẻ như dữ liệu không tập trung quanh đường thẳng \(\mathbf{h(x)}\) mà có hơi hướng theo dạng đường cong hơn. Chính vì thế nên khi sử dụng hàm \(\mathbf{h(x)}\) này, kết quả dự đoán sẽ không tốt. Khi mô hình không đáp ứng được xu hướng biến thiên của dự liệu, chúng ta có vấn đề như trên, chúng được gọi là “underfitting”. Quá trình chúng ta làm trong ML thực chất là “fit” hàm số phù hợp với sự biến thiên của dữ liệu, nên khi hàm số không biến thiên theo xu hướng của dữ liệu thì chúng chẳng hề “fit” với dữ liệu. Khi gặp vấn đề này chúng ta cần hàm số phức tạp hơn để hàm tiên đoán \(\mathbf{h(x)}\) đạt hiệu quả tốt hơn. Nếu như ta nâng \(\mathbf{h(x)}\) thành hàm bậc 2, lúc đó \(\mathbf{h(x)}\) có thể có dạng biểu diễn như sau (đường màu cam):
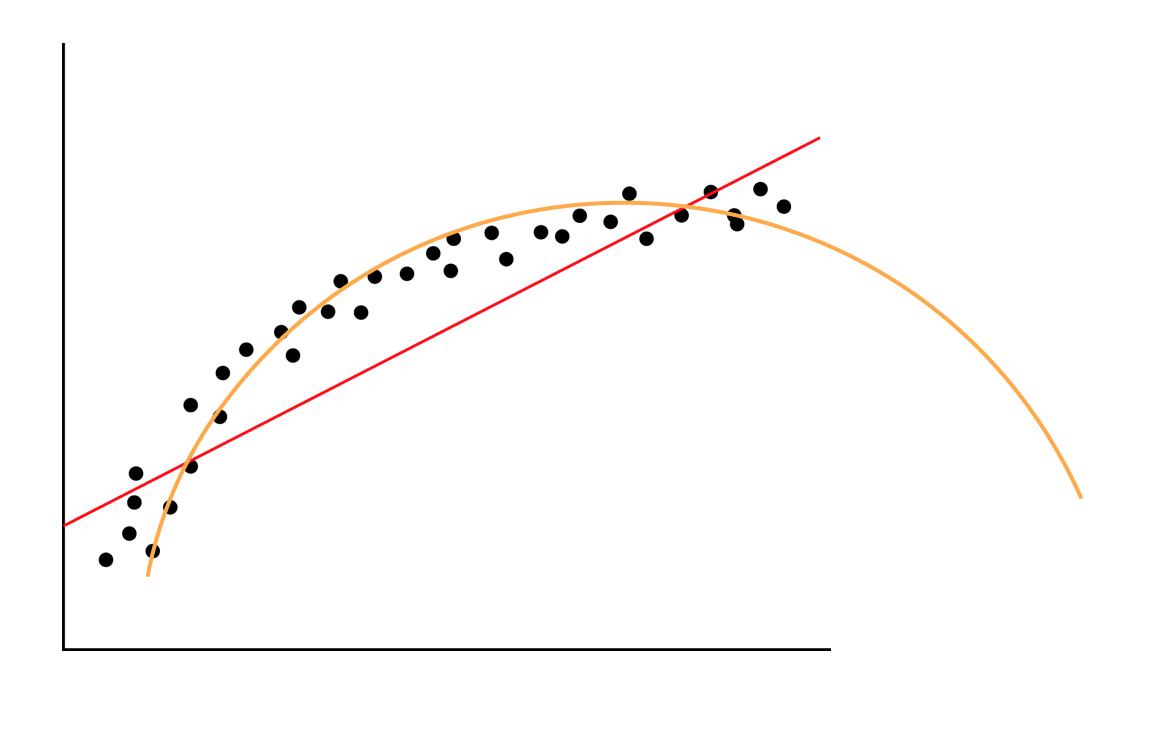
Trông có vẻ tốt hơn nhiều so với hàm bậc 1. Vấn đề đặt ra là, khi h(x) có dạng đa thức bậc cao, liệu phương pháp xây dựng \(J(\theta)\) và tối thiểu hoá \(J(\theta)\) có thay đổi gì không ?
Tin tốt là chúng không thay đổi gì cả, cụ thể khi nâng lên bậc 2: \(h(x) = \theta_0 + \theta_1x + \theta_2x^2\).
Nếu như đặt \(x_1 = x ; x_2 = x^2\) chúng ta quay về mô hình hồi quy tuyến tính.
Tương tự với bậc cao hơn, mọi hàm đa thức chúng ta đều có thể đưa về mô hình hồi quy tuyến tính.
Tuy nhiên nếu như vậy hàm số bậc càng cao thì khả năng “fit” với dữ liệu càng lớn, thậm chí sai số có thể bằng \(0\). Khi đó chúng ta sẽ gặp một vấn đề khác được gọi là “overfitting”, nhưng cách giải quyết vấn đề này tôi sẽ nói trong một bài viết sau. Với việc phát triển mô hình hồi quy tuyến tính lên đa thức bậc cao hơn, chúng ta đã bước đầu hiểu về cách ML “scale” khi gặp vấn đề phức tạp. Hi vọng các bạn có cái nhìn rõ ràng hơn về cách phát triển ML với một vấn đề, hẹn gặp lại các bạn trong bài viết tiếp theo.
