[ML – 05] Solving Classification Problem with Logistic Regression 1/2
Chào các bạn, hôm nay chúng ta tiếp tục với loạt bài về Machine Learning. Trong những bài viết trước, ta đã đề cập tới “Regression Problem” – đây là những bài toán mà đầu ra là các giá trị liên tục (nghĩa là output có thể nhận giá trị trải dài trên cả một tập số vô hạn, cụ thể trong những trường hợp thông thường là tập số thực), ở bài viết này ta sẽ đề cập tới một dạng bài toán khác “Classification Problem”.
1. Giới thiệu:
Với “Regression Problem” output của ta sẽ là giá trị liên tục (continuous value), còn với “Classification Problem” thì ngược lại, giá trị output lại là những giá trị gián đoạn (discrete value). Điều này có nghĩa là trong bài toán Classification, công việc của ta là gán nhãn cụ thể cho input, tương tự như việc phân biệt những đối tượng với nhau, chẳng hạn phân biệt một nhóm các loài động vật trong đó bao gồm “chó”, “mèo”, “lợn”, “gà” và “loại khác”.
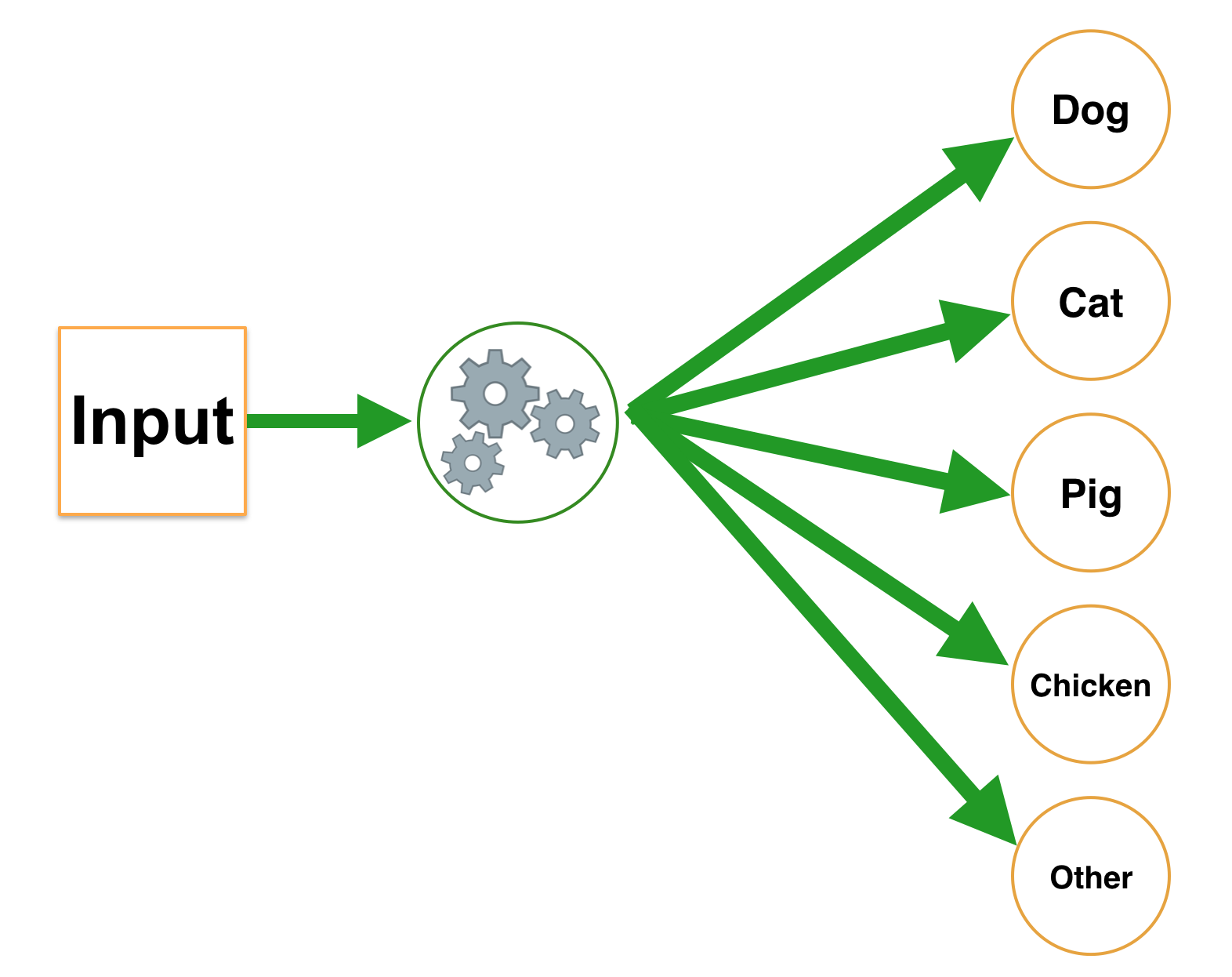
Input ở đây có thể là giá trị liên tục, chẳng hạn “cân nặng”, “chiều cao”, “tuổi thọ”,… Để giải quyết bài toán với số lượng nhãn tuỳ ý (2, 3, …), trước tiên ta sẽ giải với số lượng nhãn là \(\mathbf{2}\), sau đó tìm lời giải tổng quát cho \(\mathbf{n}\) nhãn.
2. Đơn giản hoá bài toán ?
Để đơn giản hoá bài toán, ta sẽ giải quyết nó với số lượng feature ban đầu là 1, chẳng hạn dựa vào “tuổi thọ”, dự đoán đối tượng với tuổi thọ đó là “chó” hay “mèo”.
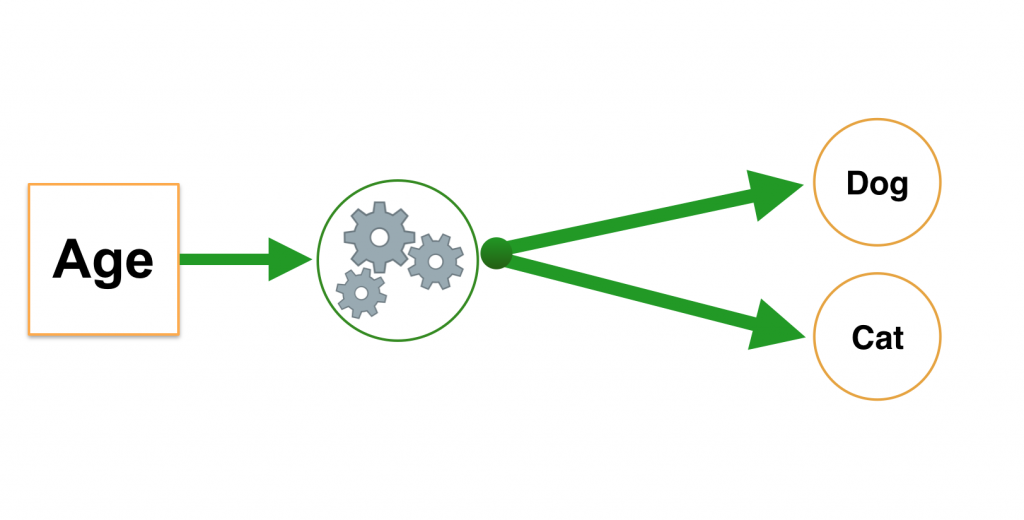
Input: age -> kiểu dữ liệu số tự nhiên nhận dữ liệu trong khoảng \([0, 100]\). Ta kí hiệu feature \(\mathbf{x}\) như với Linear Regression, \(\mathbf{x} \in [0, 100]\). Output: “dog” hoặc “cat” -> ta đánh dấu tương ứng “dog” : trả về 1 và “mèo” : trả về 0.
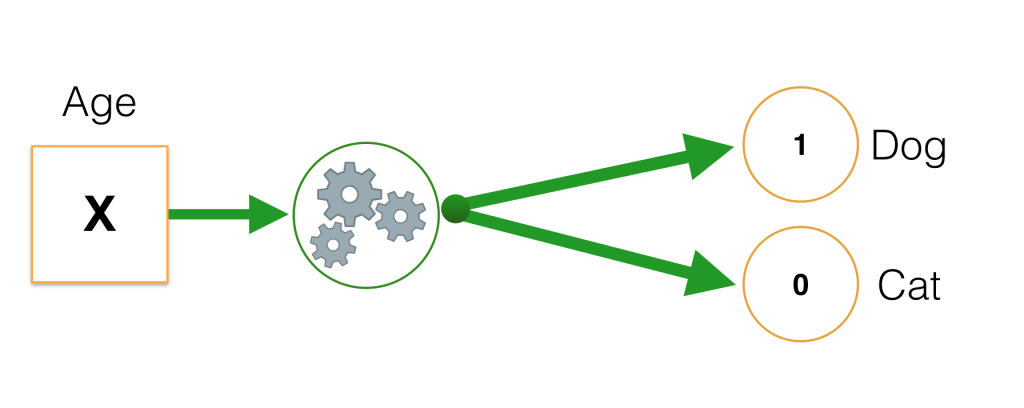
3. Linear Regression model có giải quyết được không ?
Hãy thử đưa dữ liệu lên trên đồ thị, với một feature duy nhất là tuổi thọ, ta có:
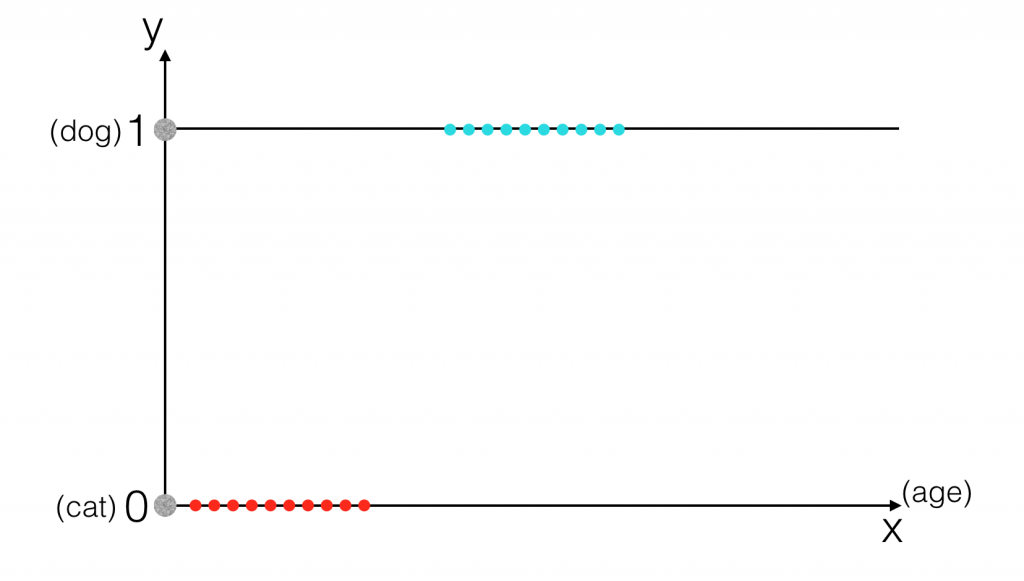
Theo tôi được biết thì có vẻ tuổi thọ của loài chó cao hơn ở loài mèo, hoặc chí ít phần lớn là như vậy, nên tuổi thọ của loài mèo (chấm đỏ) tập trung ở phía bên trái so với tuổi thọ của loài chó (chấm xanh). Trong trường hợp này trực giác cho ta thấy có lẽ ở một ngưỡng nào đó, ta có thể nhận biết được chó và mèo, nghĩa là nếu tuổi thọ vượt quá ngưỡng thì đó là chó và ngược lại. Giờ chúng ta sẽ thử áp dụng mô hình Linear Regression vào bài toán này.
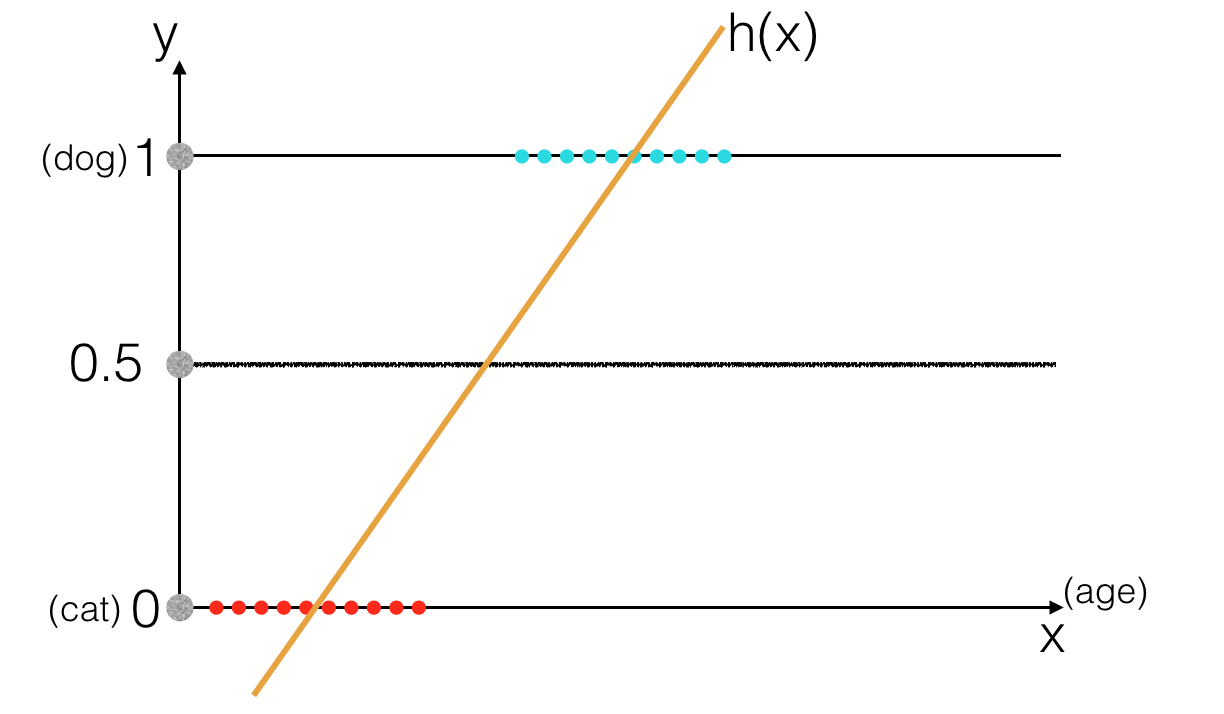
Nếu với \( h(x) \geq 0.5 \) ta gán nhãn “dog” và \( h(x) < 0.5 \) ta gán nhãn “cat” thì có vẻ trong trường hợp này Linear Regression vẫn giải quyết được vấn đề. Tuy nhiên nếu như trong tập dữ liệu training tồn tại một chú chó “ngỏm sớm” hoặc “hơi quá thọ” thì kết quả sẽ thế nào ?
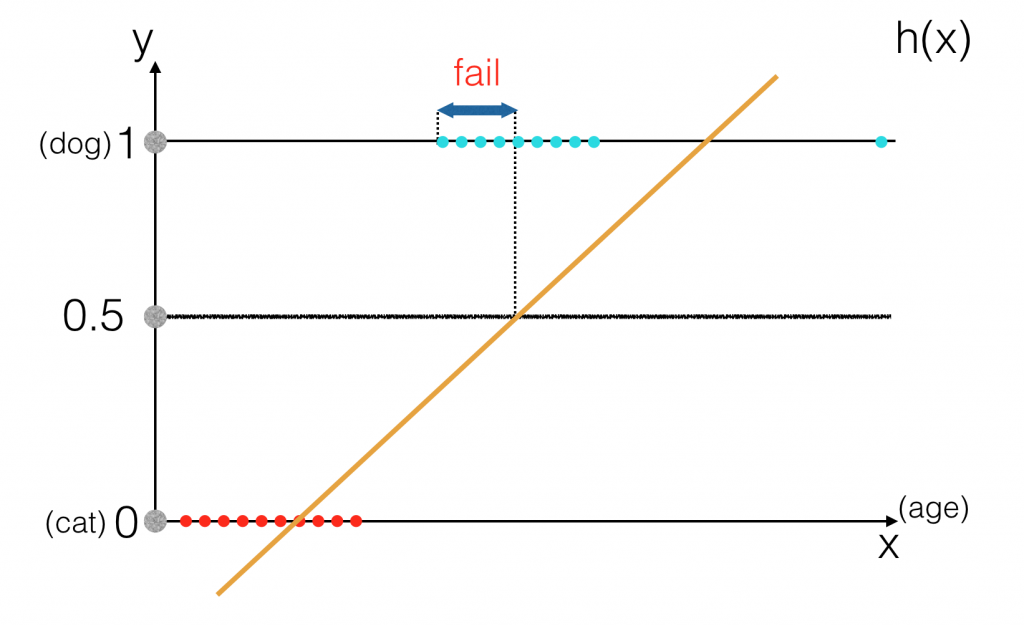
Khi đó việc so sánh \( \mathbf{h(x)} \) với ngưỡng \(\mathbf{0.5}\) sẽ không đem lại dự đoán chính xác nữa. Vậy nên ta sẽ cần một mô hình khác phù hợp hơn, đó chính là Logistic Regression. Dù cũng được gọi là Regression nhưng Logistic Regression thực sự chẳng liên quan gì tới Regression Problem, mà chỉ giải quyết Classification Problem. Vậy nên đừng sử dụng mô hình này cho Regression Problem nhé !
4. Logistic Regression:
Bài toán của ta hiện giờ như sau:
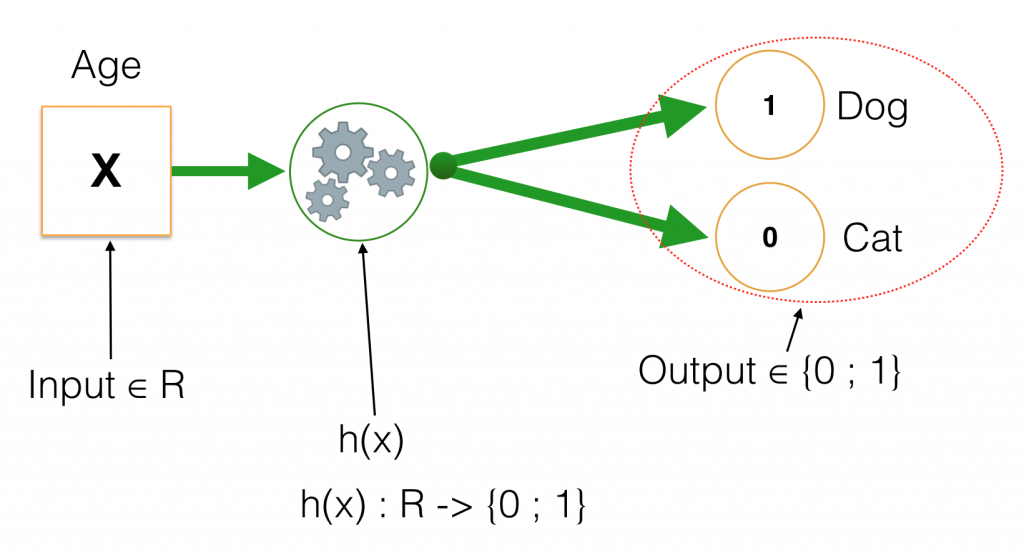
Trong đó input nhận giá trị là số thực (tổng quát là vector với các giá trị thực), còn output nhận một trong hai giá trị 0 hoặc 1. Với những hàm số thông thường (chẳng hạn những hàm đa thưc, sin, cos,…) chỉ có thể biến đổi giá trị đầu vào từ giá trị liên tục sang output cũng là giá trị liên tục. Vậy nên thay vì để output chỉ nhận hai giá trị như trên, ta tách h(x) thành 2 hàm riêng biệt. Một hàm sẽ chuyển đổi input sang R[0, 1] (Số thực trong khoảng [0, 1]), còn hàm số thứ 2 như ta thử nghiệm với Linear Regression ở trên, đặt một ngưỡng trong \( [0,1] \), nếu vượt qua ngưỡng trả về giá trị 1 và ngược lại là 0. Hàm số này được gọi là Step Function.
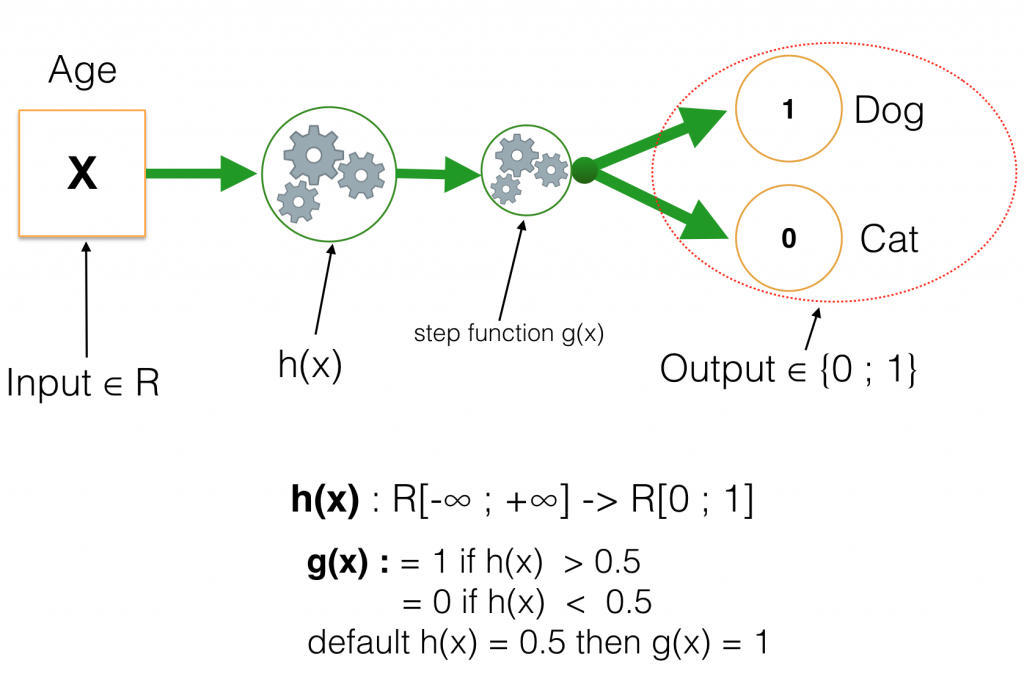
Giá trị default khi \( \mathbf{h(x)} \) có giá trị bằng chính xác ngưỡng đặt ra là tuỳ vào các bạn. Trong ví dụ này, nếu \( h(x) = threshold \) (ngưỡng) thì kết quả trả về là 1. Nếu để ý một chút, ta sẽ thấy giá trị nằm trong [0, 1], đây chính là xác suất xảy ra y = 1, Hay nói cách khác \(h(x) = P(y = 1)\). Nghĩa là ta đi xây dựng hàm số tính xác suất đối tượng có nhãn là “dog”, nếu xác suất \(\geq 0.5 \) thì gán nhãn “dog” và ngược lại. Và vì đối tượng cần kiểm tra chỉ là “dog” or “cat” nên ta có xác suất \(P( y = 0 ) + P( y = 1 ) = 1\).
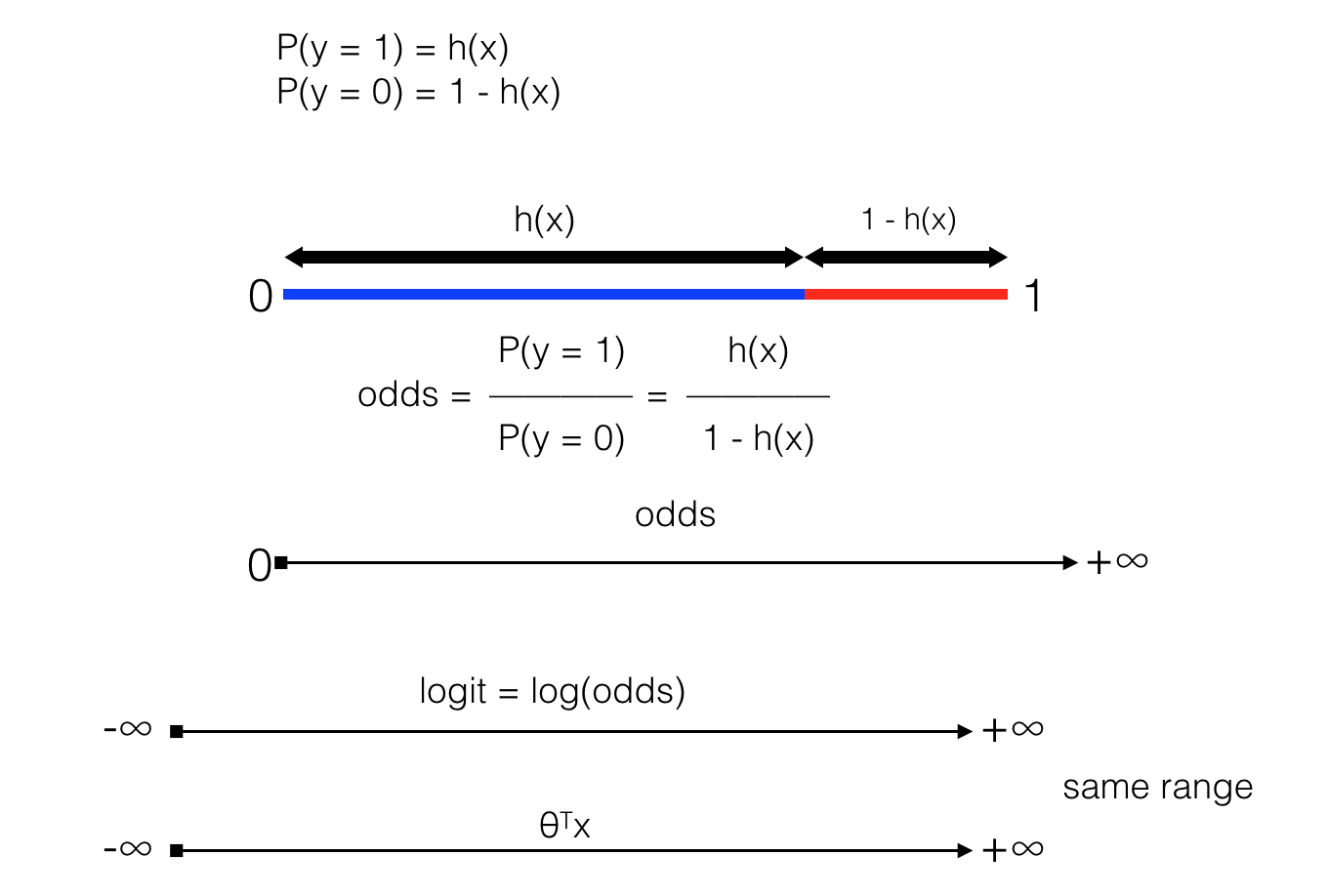
Xác suất là tỉ lệ giữa số lần xảy ra và số lần thử nghiệm, tuy nhiên khi phép thử chỉ có 2 khả năng thì chúng ta còn có một đại lượng khác để đánh giá khả năng xảy ra của một biến cố, được gọi là odds (hay ratio). Trong bài toán này, ta có odds được tính như hình trên Khi ((odds = 1\) -> nghĩa là \(h(x) = 1 – h(x)\). Đây chính là giá trị ngưỡng mà ta đặt ra. Khi \(odds > 1\) -> \(h(x) > 1 – h(x)\) ; khi odds càng lớn thì h(x) càng lớn so với \(1 – h(x)\) hay \(h(x)\) càng tiến gần tới \(1\) -> xác suất \(y = 1\) cao. Khi \(odds < 1\) -> \(h(x) < 1 – h(x)\) hay xác suất \(y = 0\) cao. Bên cạnh đó Logarit của một số nguyên dương có giá trị trong khoảng [-∞ , +∞], nên nếu lấy logarit của odds (được gọi là logit) ta sẽ có một đại lượng biến thiên như \(\theta ^Tx\) (trong mô hình Linear Regression). Chú ý rằng khi input là vector thì \(\theta\) cũng là vector, nên \(\theta x\) phải được viết là \(θ^Tx\) (nghĩa là matrix chuyển vị \(\mathbf{θ}\) nhân với vector \(\mathbf{x}\), vector là một trường hợp đặc biệt của matrix). Vậy nên ta có thể đặt tham số và input vào logit để máy có thể học được từ dữ liệu \[=> logit(odds) = \theta ^Tx\] Biến đổi một chút ta sẽ có hàm số của \(h(x)\):
\[\begin{align*} \\ & odds = \frac{P(y = 1)}{P(y = 0)} \\ & odds = \frac{h(x)}{1-h(x)} \\ & => log(odds) = log(\frac{h(x)}{1-h(x)})\\ & => \theta^{T}x = log(\frac{h(x)}{1-h(x)})\\ & => e^{\theta^{T}x} = \frac{h(x)}{1-h(x)}\\ & => e^{\theta^{T}x}(1-h(x)) = h(x)\\ & => e^{\theta^{T}x} = h(x)(1+e^{\theta^{T}x})\\ & => h(x) = \frac{e^{\theta^{T}x}}{1 + e^{\theta^{T}x}}\\ & => h(x) = \frac{1}{1 + e^{-\theta^{T}x}} \end{align*}\]\(\theta^{T}x\) là dạng tuyến tính, nên cũng như Linear Regression ta có thể phát triển Logistic Regression với những thành phần đa thức (tương tự phát triển Linear Regression -> Polynomial Regression).
Vấn đề đặt ra của ta bây giờ là làm sao để xây dựng cost function cho \( \mathbf{h(x)} \), nếu như tương tự như Linear Regression \(J(\theta) = (h(x) – y)^2\) (Least Mean Square) nhưng các bạn cũng thấy \( \mathbf{h(x)} \) khá phức tạp nên việc tính đạo hàm cho \( J(\theta) \) sẽ không hề đơn giản. \[ J(\theta) = (\frac{1}{1 + e^{-\theta^{T}x}} - y)^2 \] Trong bài viết sau chúng ta sẽ xây dựng \( \mathbf{J(θ)} \) theo một cách khác. Hẹn gặp lại các bàn trong bài viết tiếp theo !
