[ML – 06] Solving Classification Problem with Logistic Regression 2/2
Hôm nay chúng ta tiếp tục phần bài về Logistic Regression, cụ thể ta sẽ đi xây dựng cost function \( \mathbf{J(θ)} \) cho \( \mathbf{h(x)} \).
5. How to build cost function in Logistic Regression ?
Nhắc lại về \( \mathbf{h(x)} \): \[ h_{\theta}(x) = g(\theta^{T}x) = \frac{1}{1 + e^{-\theta^{T}x}} \] Trong đó: \[ g(z) = \frac{1}{1 + e^{-z}} \]
Trong đó \( \mathbf{g(z)} \) được gọi là sigmoid function (trường hợp đặc biệt của logistic function). Đây là một trong những hàm được sử dụng phổ biến trong ML, dạng biểu diễn trên đồ thị như sau:
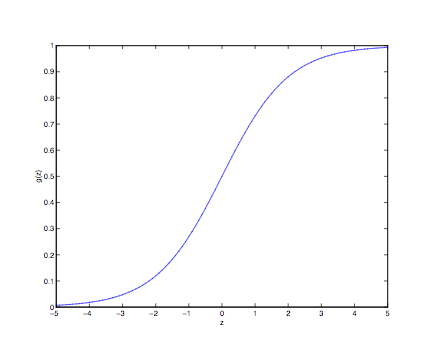
Như đã nói trong bài viết trước, vì \( \mathbf{h(x)} \) trả về giá trị trong khoảng \([0 , 1]\) mà \(y\) chỉ nhận một trong hai giá trị \({0;1}\) nên ta coi như xác suất để \(y = 1\) (với điều kiện đã có \(\mathbf{x}\) và \(\mathbf{\theta}\)) là \( \mathbf{h(x)} \), xác suất để \(y = 0\) là \( \mathbf{1 - h(x)} \) (với điều kiện đã có \( \mathbf{x} \) và \( \mathbf{\theta} \)): \[P(y = 1 ⎮ x;\theta) = h_{\theta}(x)\] \[P(y = 0 ⎮ x;\theta) = 1 – h_{\theta}(x)\] Ta viết \(h_{\theta}(x)\) vì xác suất sẽ thay đổi không chỉ khi \( \mathbf{x} \) thay đổi mà cả \( \mathbf{\theta} \) thay đổi. Bên cạnh đó ta có thể viết một cách gọn nhẹ phân phối xác suất của \( \mathbf{y} \) bằng một hàm duy nhất như sau: \[P(y ⎮ x;\theta) = (h_{\theta}(x)) ^{y}(1 – h_{\theta}(x))^{1 – y}\] Các bạn chỉ cần thay \(y = 0\) và \(y = 1\) sẽ thấy hàm số trên đại diện cho xác suất cho cả hai trường hợp. Do y chỉ nhận hai giá trị nên hàm số trên chính là hàm phân phối xác suất của y (tuân theo phân phối Bernoulli) Giả sử trong tập training của ta có \( \mathbf{m} \) training examples, được thu thập một cách độc lập, không phụ thuộc vào nhau. Vì vậy xác suất để mô hình dự đoán chính xác với mỗi cặp \(\mathbf{(x,y)}\) cũng tuân theo hàm phân phối xác suất trên \[P(y^{(i)} ⎮ x^{(i)};\theta) = (h_{\theta}(x^{(i)}))^{y^{(i)}}(1 – h_{\theta}(x^{(i)}))^{1 – y^{(i)}}\]
(Trong đó \(x^{(i)}\) và \(y^{(i)}\) là cặp data thứ \(i\) trong tập \(m\) data) Suy ra xác suất để mô hình dự đoán được chính xác của \(m\) training examples là:
\[\begin{align*} L(\theta) & = p(\overrightarrow{y} | X ; \theta)\\ & = \prod_{i=1}^{m}p(y^{(i)} | x^{(i)} ; \theta)\\ & = \prod_{i=1}^{m}(h_{\theta}(x^{(i)}))^{y^{(i)}}(1 - h_{\theta}(x^{(i)}))^{y^{(i)}} \end{align*}\]Kí hiệu \(\overrightarrow{y}\) là đại diện cho tất cả y trong tập training, nghĩa là \(L(θ)\) là xác suất để mô hình dự đoán đúng toàn bộ y trong tập training. Chính vì thế nên để mô hình ít sai số nhất (error thấp nhất) ta cần cực đại hoá \(L(θ)\) hay cực đại hoá xác suất xảy ra tất cả \(y^{(i)}\) trong tập training. Phương pháp này gọi là Maximize Likelihood Estimation (MLE), chú ý một chút là nếu áp dụng phương pháp này vào Linear Regression (LR) các bạn sẽ thu được kết quả tương tự với Least Mean Square chỉ khác là LR tuân theo phân bố Gaussian chứ không phải Bernoulli như Logistic Regression. Quay trở lại với vấn đề MLE, để maximize \(L(θ)\) ta có thể chỉ cần maximize \(log(L(θ))\) vì hàm mũ tăng giảm tương tự như số mũ (giá trị hàm mũ thường tăng nhanh hơn, nhưng giống nhau về xu hướng tăng giảm). Các bạn có thể kiểm chứng bằng tính đạo hàm của một số và log của nó sẽ thấy chúng cùng \(> 0\) và \(< 0\) tại mọi thời điểm. Chính vì lẽ đó nên người ta thường maximize \(log(likelihood)\) thay vì trực tiếp với likelihood (do hàm log sẽ triệt tiêu các số mũ).
\[\begin{align*} \\ l(\theta) & = log(L(\theta))\\ & = \sum_{i=1}^{m}y^{(i)}log(h(x^{(i)})) + (1-y^{(i)})log(1 - h(x^{(i)})) \end{align*}\]Giải thích một chút rằng: \[log(\mathbf{a} * \mathbf{b}) = log(\mathbf{a}) + log(\mathbf{b})\] \[log(\mathbf{a}^{\alpha}) = \alpha * log(\mathbf{a})\] Nếu muốn kiểm chứng các bạn hãy đặt bút tính thử nhé :). Và đây cũng chính là cost function của \(h(x)\), một cách viết khác dài dòng hơn của nó như sau:
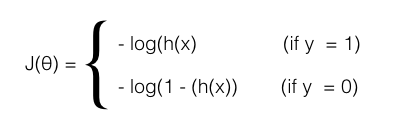
6. Applying Gradient descent to minimize cost function:
Chúng ta sẽ không nhắc lại chi tiết về giải thuật Gradient descent, trong trường hợp các bạn quên thì hãy quay về bài ML-03 để xem nhé. Để áp dụng giải thuật này, công việc của chúng ta chỉ là đi tính đạo hàm của \(J(θ)\), trong trường hợp này chính là log của likelihood:
\[\begin{align*} \\ \frac{\partial}{\partial \theta_{j}}l(\theta) & = (y\frac{1}{g(\theta^{T}x)} - (1-y)\frac{1}{1-g(\theta^{T}x)})\frac{\partial}{\partial \theta_{j}}g(\theta^{T}x)\\ & = (y\frac{1}{g(\theta^{T}x)} - (1-y)\frac{1}{1-g(\theta^{T}x)})g(\theta^{T}x)(1-g(\theta^{T}x))\frac{\partial}{\partial \theta_{j}}\theta^{T}x\\ & = (y(1-g(\theta^{T}x)) - (1-y)g(\theta^{T}x))x_{j}\\ & = (y - h_{\theta}(x))x_{j} \end{align*}\]trong đó đạo hàm của hàm sigmoid \(g(z)\):
\[\begin{align*} \\ g'(z) & = \frac{\partial}{\partial z}\frac{1}{1 + e^{-z}}\\ & = \frac{1}{(1 + e^{-z})^{2}}(e^{-z})\\ & = \frac{1}{1 + e^{-z}}(1 - \frac{1}{1 + e^{-z}})\\ & = g(z)(1 - g(z)) \end{align*}\]Các bạn có thể dễ dàng kiểm tra lại phép diễn giải trên. Như vậy ta đã có đạo hàm của \(J(θ)\) trông khá giống với đạo hàm cost function của Linear Regression nhưng điểm khác nhau ở đây là \(h(x)\) không còn là hàm tuyến tính, mà hàm sigmoid. Giải thuật sẽ trông giống như ở Linear Regression nếu như ta không viết cụ thể \(h(x)\).
\[\theta_{j} := \theta_{j} – \alpha(h_{\theta}(x^{(i)}) – y^{(i)}) x^{(i)}_{j}\]
7. Decision Boundary:
Đến đây thì các bạn đã biết hàm sigmoid là gì, xây dựng nó như thế nào, và tại sao. Giờ ta sẽ xem thêm một chút về hình ảnh trực quan về cách dữ liệu được phân biệt như thế nào. Trong mô hình Logistic Regression, dữ liệu được phân tách các loại bởi một hàm số. Cụ thể: \[h(x) > 0.5 => y = 1\] \[h(x) < 0.5 => y = 0\] có nghĩa \(h(x) = 0.5\) là ngưỡng phân biệt giữa \(y = 0\) và \(y = 1\). Hay nói cách khác hàm số \(h(x) = 0.5\) chính là đường ranh giới giữa những dữ liệu \(y = 0\) và \(y = 1\) (được gọi là Decision Boundary)
\[\begin{align*} h(x) & = 0.5\\ => \frac{1}{1 + e^{\theta^{T}x}} & = 0.5\\ => \theta^{T}x & = 0 \end{align*}\]Khi ta biểu diễn dữ liệu chỉ với các trục của \(x\) (không bao gồm \(y\)), chẳng hạn trên dữ liệu chỉ có 2 features ta có:
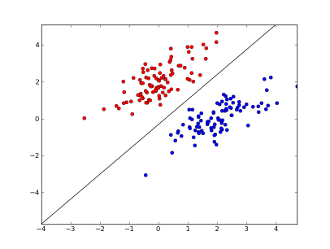
Trong trường hợp này, \(\theta^{T}x\) chỉ là hàm tuyến tính nên đường ranh giới chỉ là đường thẳng. Nếu như \(\theta^{T}x\) có dạng \(x_1^2 + x_2^2\) thì decision boundary sẽ như hình sau:
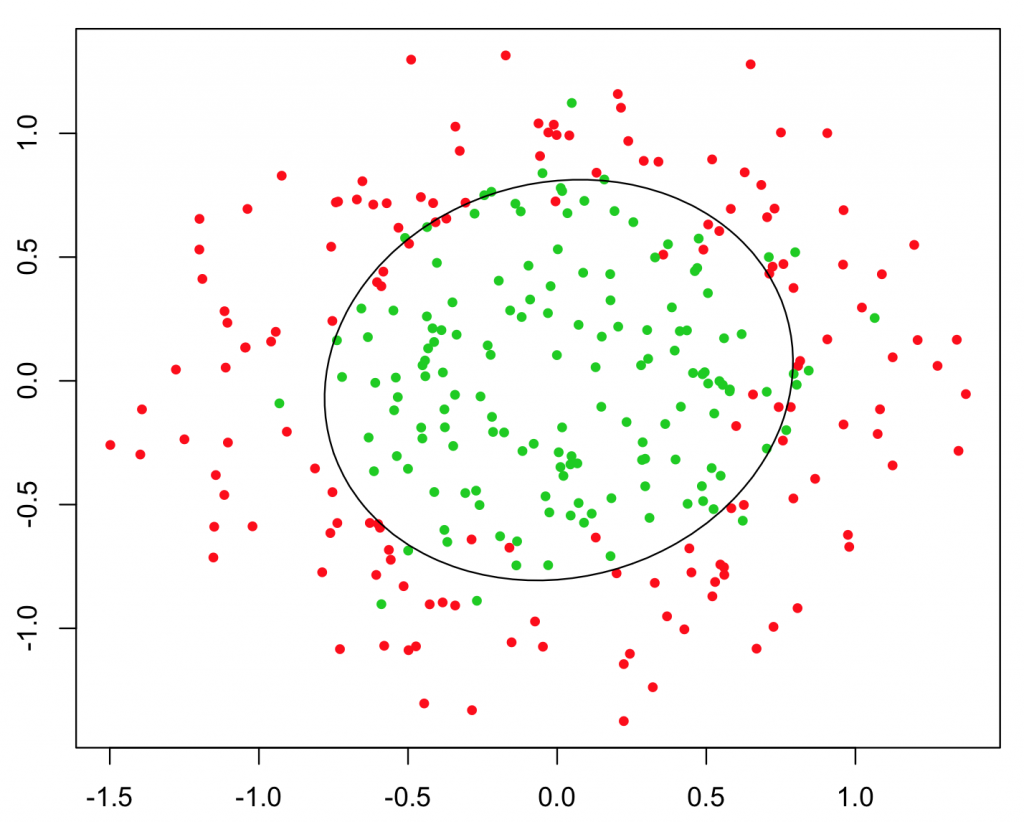
\(\theta^{T}x\) càng phức tạp, càng có bậc cao.. thì decision boundary càng phức tạp và mô tả được sự phân tách đối với những tập dữ liệu khó phân biệt hơn. Chỉ với dạng tuyến tính, ta cũng có thể xây dựng được mô hình để phân biệt các kí tự với nhau, tuy chưa quá tốt nhưng cũng không hề tệ, sau đây là ví dụ tôi đã làm để điện thoại có thể nhận diện được số “2” và “không phải số 2”:
Trong ứng dụng demo trên, tôi hứng các điểm chạm của người dùng, trình bày chúng trên một matrix \(10×10\) và sử dụng Logistic Regression với input là \(10 * 10 = 100\) giá trị của matrix. Training một thời gian mô hình sẽ cho ta nhận diện được một kí tự bất kì có phải là kí tự ta cho nó học không (trong video trên là số 2).
8. Logistic Regression for multiclass:
Trong trường hợp mô hình logistic regression có nhiều output. Khi đó ta chỉ cần số hàm \(h(x)\) như số output, mỗi hàm \(h(x)\) sẽ đảm nhiệm phân biệt có phải đối tượng của nó hay không. Cụ thể ta ví dụ phân biệt các chữ số:
- \(h_{0}\) sẽ phân biệt có phải chữ số 0 hay không ?
- \(h_{1}\) sẽ phân biệt có phải chữ số 1 hay không ?
- \(h_{2}\) sẽ phân biệt có phải chữ số 2 hay không ?
- …
- \(h_{9}\) sẽ phân biệt có phải chữ số 9 hay không ?
output trả về sẽ là một vector \([y_0, y_1, y_2, … , y_9]\) nếu vector có giá trị 1 ở tham số nào thì mô hình kết luận đó là chữ số đó. Trong trường hợp tất cả là 0 thì đây không phải chữ số nào cả. Phương pháp này được gọi là one-rest, đánh giá từng class so với tất cả các class còn lại.
