[ML – 07] Understanding Neural Network 1/3
Trong các bài viết trước, ta đã học về 2 mô hình cơ bản trong ML là “Linear Regression” và “Logistic Regression” để giải quyết 2 vấn đề thường gặp là “Regression Problem” và “Classification Problem”. Tiếp theo chúng ta sẽ tìm hiểu về Artificial Neural Network (ANN) hay mạng nơ ron nhân tạo. Trước khi đi sâu vào tìm hiểu ANN là gì, ta sẽ đi tìm câu trả lời cho câu hỏi “Tại sao lại cần ANN ?”
1. Why do we need ANN ?
Như đã nói ở trên, ta đã biết về 2 mô hình cơ bản trong ML có thể dùng để giải quyết được 2 vấn đề thường gặp là “Regression Problem” và “Classification Problem”, đồng thời ta cũng đã biết cách mở rộng 2 mô hình trên bằng cách thêm những thành phần đa thức “polynomial” để có được mô hình phức tạp hơn tiệm cận đến pattern của dữ liệu. Vậy tại sao chúng ta lại cần tới ANN ? Hãy lấy ví dụ với Logistic Regression, trong đó ta có dữ liệu như sau:

Ở ví dụ trên, ta không chỉ thuần thuý sử dụng một đường thẳng để phân chia 2 loại dữ liệu mà cần một đường cong có hình dạng phức tạp để có được mô hình chính xác hơn. Chẳng hạn như sau:

Các bạn cũng biết đồ thị có bao nhiêu điểm đạo hàm đổi dấu (hay đoạn cong) tương đương với số bậc của hàm số, chính vì thế với đường ranh giới phức tạp như trên có thể sẽ đòi hỏi nhiều thành phần đa thức được thêm vào. Trong trường hợp này chúng ta chỉ có 2 feature, nên khi tăng lên bậc 2 chỉ phải thêm \(x_1x_2 ; x_1^2 ; x_2^2,\) và bậc 3 là : \(x_1^3 ; x_2^3 ; x_1^2x_2 ; x_2^2x_1,\) …. Số lượng feature được thêm vào tăng theo hàm mũ \(O(n^m)\) trong đó \(\mathbf{n}\) là số lượng feature và \(\mathbf{m}\) bậc, nếu như ta chỉ có vài feature thì số lượng feature đa thức thêm vào sẽ vẫn chấp nhận được tuy nhiên trên thực tế số lượng feature chẳng bao giờ nhỏ cả. Đặc biệt nếu như chúng ta muốn xử lý vấn đề về “Computer Vision”. Cụ thể khi với một tấm ảnh sau:

Với con người ta dễ dàng nhận biết đây là một con mèo, nhưng máy tính không nhìn mọi thứ như chúng ta thấy mà chỉ toàn các con số :

Mỗi điểm trên tấm ảnh sẽ được mô tả bởi một hay vài tham số, chẳng hạn với ảnh binary thì chỉ gồm 1 số 0 hoặc 1 đại diện cho màu trắng hoặc đen, với ảnh gray scale cũng chỉ gồm 1 số nhưng thay đổi trong khoảng \([0; 255]\) đại diện cho độ tối của điểm ảnh, với ảnh RGB lại cần tới 3 tham số R, G, B đại diện cho 3 màu Red, Green, Blue. Ta thử tưởng tượng mỗi tấm ảnh chỉ cần bé bé xinh xinh cũng chứa hàng trăm điểm ảnh (20×30 là 600 điểm), mà input cho tấm ảnh sẽ là những thuộc tính của điểm ảnh nên với số lượng feature tuyến tính, chúng ta đã phải đưa vào hàng trăm đến hàng triệu feature. Nếu như thêm vào các thành phần đa thức thì số lượng feature sẽ tăng lên đáng kể, vượt quá sức chịu đựng của máy tính hiện nay, khiến cho thời gian training dài, thậm chí không khả thi. Vậy nên để đối phó với vấn đề này, chúng ta cần mô hình khác, hiệu quả hơn.
2. Neurons and the brain :
Neural Networks (NNs) được lấy cảm hứng từ việc mong muốn xây dựng được những loại máy có khả năng mô phỏng theo cách thức làm việc của bộ não con người. Vậy tại sao chúng ta lại không xây dựng một hệ thống học dựa trên sự bắt chước não bộ con người ? Chính vì thế ANN ra đời! Trong những năm thập niên 80, 90, ANN được sử dụng rất nhiều cho đến cuối những năm 90 khi mà ANN không còn khả thi nữa do giới hạn về phần cứng máy tính. Tuy nhiên, gần đây với sự phát triển chóng mặt của phần cứng, tốc độ máy tính được cải thiện đáng kể, ổ cứng flash, ram với dung lượng lớn hơn nhiều, chip được tăng tốc độ đáng kể. Bản thân việc tính toán trên NN cũng rất tốn kém, nên chỉ dạo gần đây những NN lớn mới trở nên khả thi (như Google đã xây dựng NN với 16000 neurons). Brain – não bộ, một “bộ máy” tinh vi có thể làm được rất nhiều thứ “điên rồ”. Mặc dù chưa thể khám phá được những điều kì diệu ẩn sâu bên trong não bộ của con người, nhưng ta có thể giả thuyết rằng bộ não của chúng ta chỉ có một giải thuật học tập duy nhất (chứ không phải mỗi giải thuật giải quyết một vấn đề như chúng ta đã được học trong ML). Có một vài bằng chứng cho giả thuyết trên như sau:
- Phần thính giác của não bộ dùng để nhận tín hiệu âm thanh, nhưng nếu như ta cắt bỏ đường truyền tín hiệu từ tai đến phần não này, sau đó nối phần thính giác với phần thần kinh thị giác phía sau 2 con mắt thì khi đó phần thính giác này vẫn có thể học để nhìn.
- Phần xúc giác của não bộ dùng để nhận biết những tín hiệu truyền từ các tế bào xúc giác nằm dưới da của ta, nếu như làm tương tự như trên nối phần xúc giác này với phần thần kinh thị giác thì nó vẫn có thể học để nhìn.
Vậy nên có lẽ, tất cả các phần trong bộ não của chúng ta đều học cùng một kiểu hay bộ não tự bản thân nó học làm sao để học. Vì vậy đích đến của ML là xây dựng được giải thuật học có thể giải quyết được mọi vấn đề mà không cần thiết kế phát triển lại.
3. ANN: representation of a neuron ?
Trong mạng neuron nhân tạo, mỗi neuron là một hàm số (như hàm tuyến tính hay hàm sigmoid). Chúng ta sẽ mô tả ANN với mỗi neuron là một hàm sigmoid. Với 1 neuron duy nhất, chúng ta có ANN là một hàm logistic:

Trong đó:

Với k output:
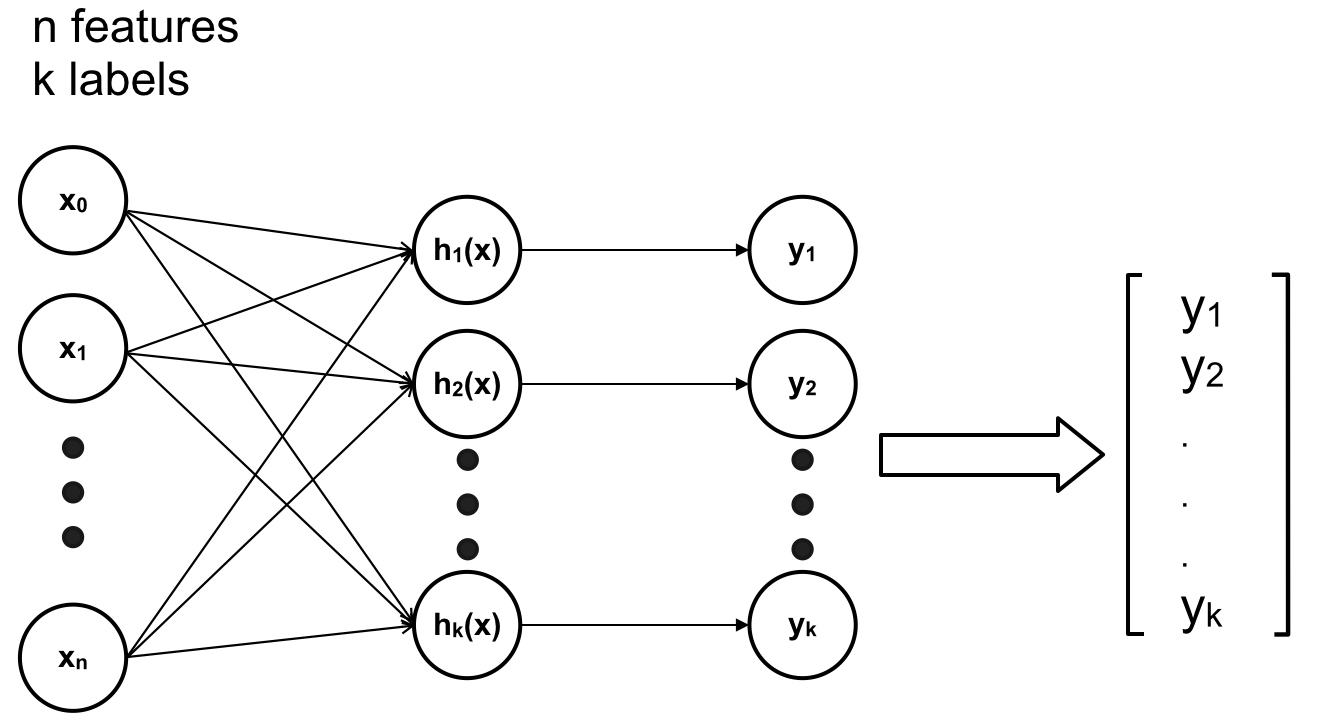
Trong những trường hợp trên ANN của chúng ta chỉ gồm 1 lớp Input (Input Layer – gồm các feature \(x\)) và 1 lớp output (Output Layer – gồm các \(h(x)\)).
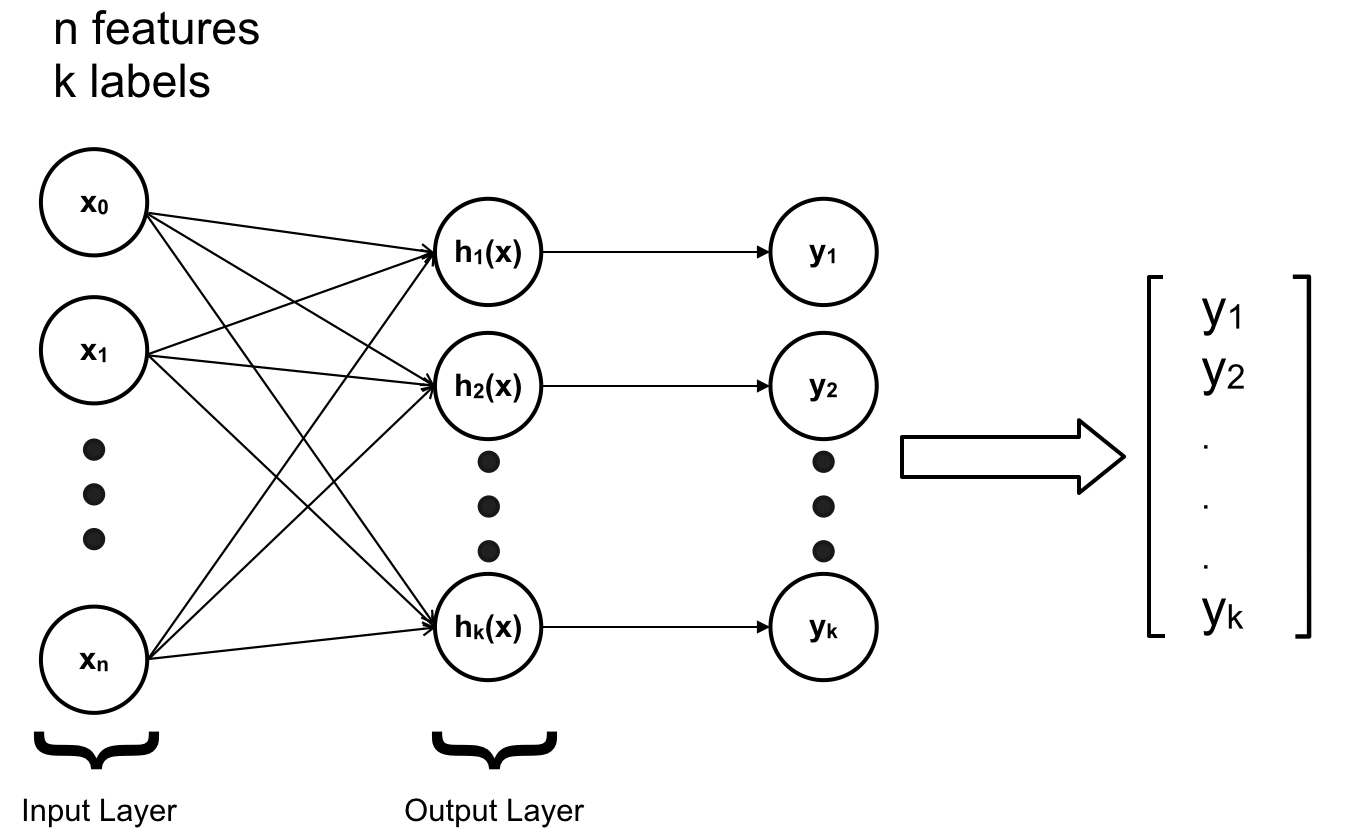
Bias ở đây chính là những giá trị như \(x_0 = 1\).
Mỗi layer trong ANN có thể có một hay nhiều neuron (tương ứng ta có thể có nhiều feature, nhiều output, nhiều h(x)..). Input Layer và Output Layer chỉ có một, riêng Hidden Layer có thể có nhiều, số lượng Hidden Layer sẽ khiến cho độ phức tạp của mô hình thay đổi. Khi đó ta không cần thêm quá nhiều thành phần đa thức vào các feature để khiến cho mô hình đủ phức tạp để fit với dữ liệu.
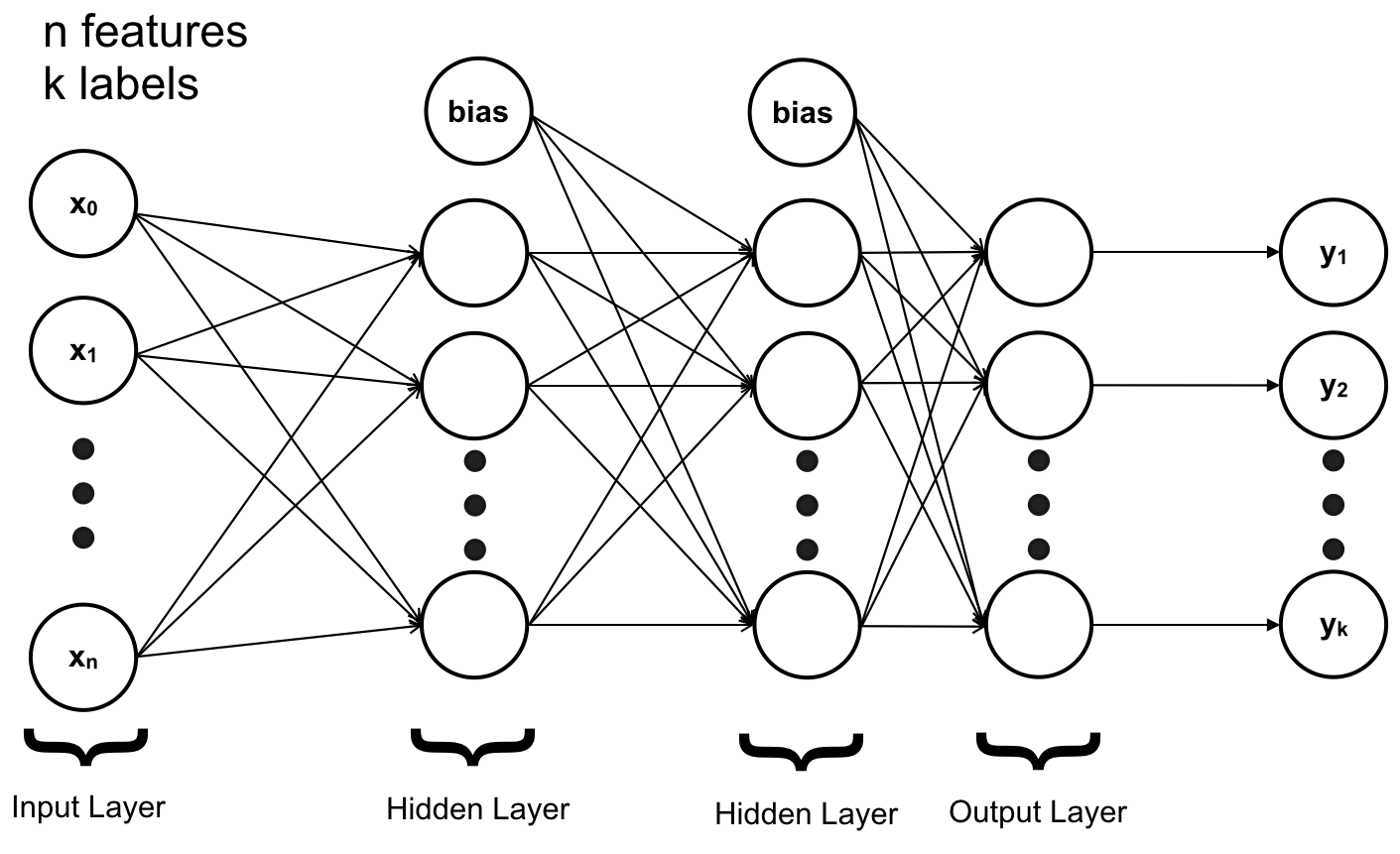
4. Neural Networks – Notation:
Để tiện cho việc phát triển mô hình và tránh để các bạn nhầm lẫn, chúng ta sẽ dành một chút thời gian để thống nhất các kí hiệu được sử dụng ở đây: Thay vì phân biệt các layer, ta đánh số các layer, bắt đầu từ Input Layer là layer 1, Hidden Layer là \(2, 3, .., L – 1,\) Output Layer là \(L\). Nghĩa là ANN của chúng ta có tổng cộng L (layers)
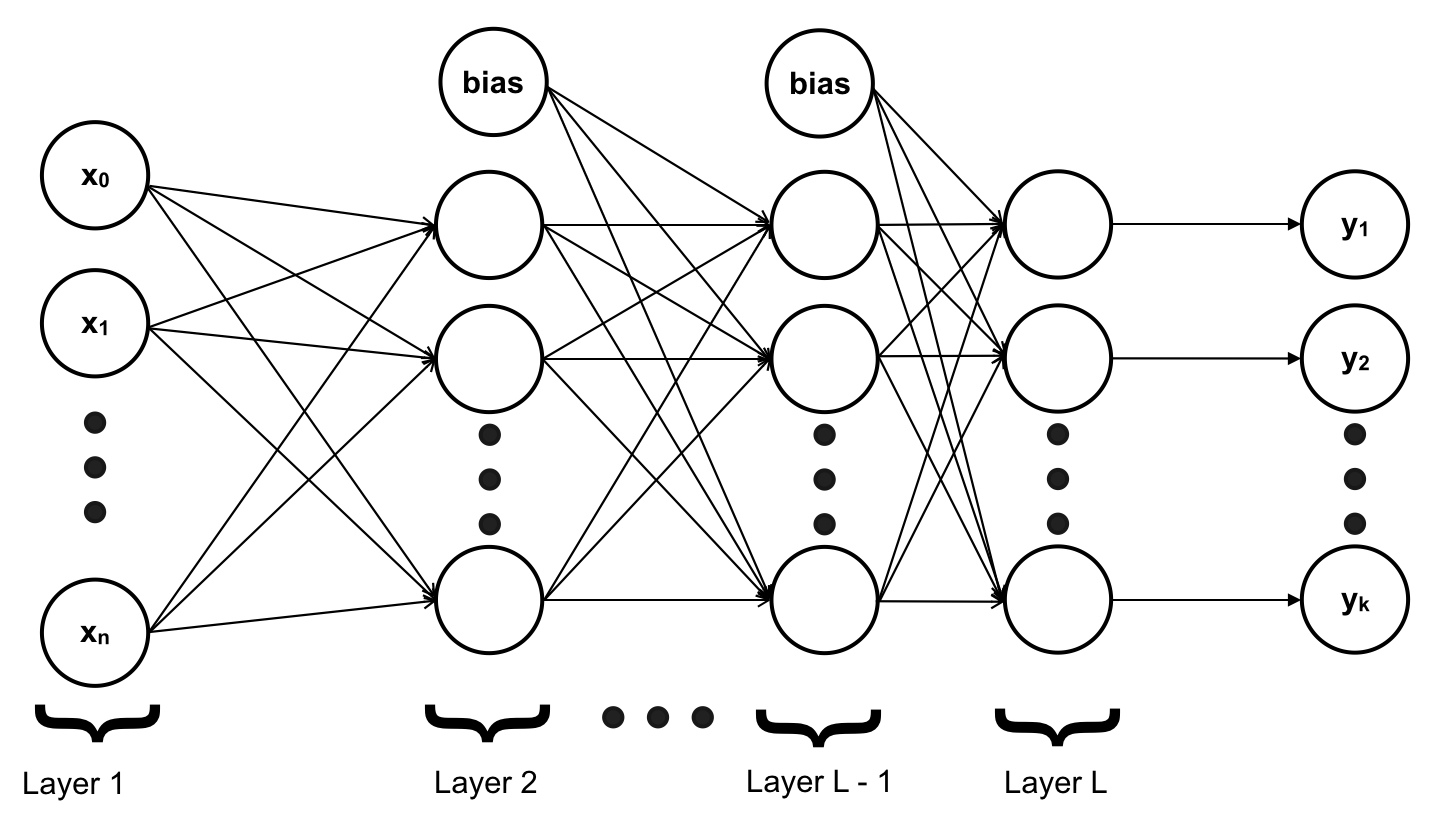
\(a_{i}^{(j)}\) – activation of unit \(i\) layer \(j\) (hàm activation của neuron thứ \(i\) của layer thứ \(j\)). Trong ví dụ đề cập đến trong bài viết này, \(a\) chính là một hàm sigmoid. Vì lúc này một hàm sigmoid không còn quyết định được output của mô hình nữa mà chỉ tạo ra output là input của layer kế tiếp. Do đó chỉ duy nhất những hàm activation của Output Layer mới được gọi là hypothesis \(h(x)\). \(a_1^{(2)}\) là hàm activation của neural hay unit thứ 1 của layer thứ 2 \(a_0^{(2)}\) đúng ra là hàm activation của unit thứ 0 của layer 2 nhưng đây chỉ là giá trị bias tương tự như \(x_0\) nên nó chỉ là giá trị bias của layer 2 và có giá trị = 1. Thường được kí hiệu “+1” trên mô hình.
\[a_0^{(1)} = x_0\\ a_1^{(1)} = x_1\\ …\]\(s_ℓ\) là số lượng neuron hay unit của layer \(ℓ\) không tính giá trị bias
\(s_1\) là số lượng neuron hay unit của layer 1 không tính giá trị bias
\(s_2\) là số lượng neuron hay unit của layer 2 không tính giá trị bias

Vì ta có \(k\) label cần phân biệt nên có \(k\) output và output layer hay layer thứ L sẽ có \(k\) neurons => \(s_L = k\)
\(\theta_j\) là matrix các tham số để chuyển đổi giữa input thu được từ output của layer liền trước thành output để layer kế tiếp có thể sử dụng. Tương tự như \( \theta \) trong \(\theta^{T}x\) thì \(\theta\) là vector chuyển hoá vector input \(x\) sang output, tuy nhiên vì ở đây mỗi layer chúng ta có nhiều hơn một hàm activation nên \(\theta\) phải là một matrix. Chúng ta sẽ đi sâu hơn khi nói về cách ANN tính toán. Trong ví dụ ở đây tất cả các hàm activation đều là hàm sigmoid nên:

Trong đó:

5. Forward Propagation:
Đặt \(z\) là hàm tuyến tính, thì với mỗi hàm \(z\) ta có tương ứng một hàm activation \(g\):
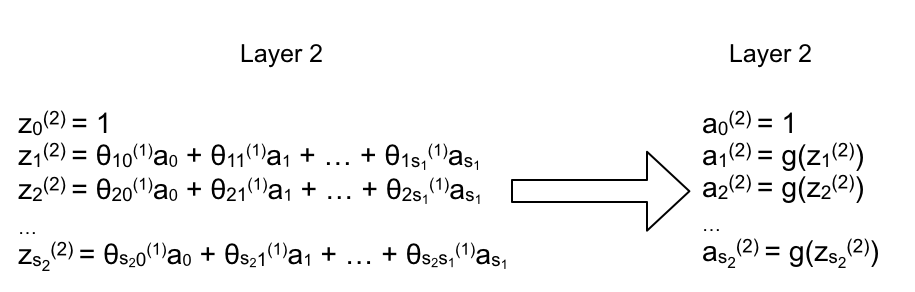
Kí hiệu các chỉ số trên \(z\) cũng tương tự như \(a\), trong trường hợp hàm activation \(a\) là hàm tuyến tính thì \(a\) chính là \(z\). Ta sẽ đi vector hóa \(z\) – nghĩa là tính \(z\) cho cả một layer dưới dạng vector thay vì cho từng unit (neuron).

Do \(a_0 = 1\) được thêm vào tại mỗi layer chứ không phải được tính dựa trên layer trước đó nên ta không đưa vào vector trên để tránh nhầm lẫn. Những unit còn lại được tính dựa vào layer trước đó:
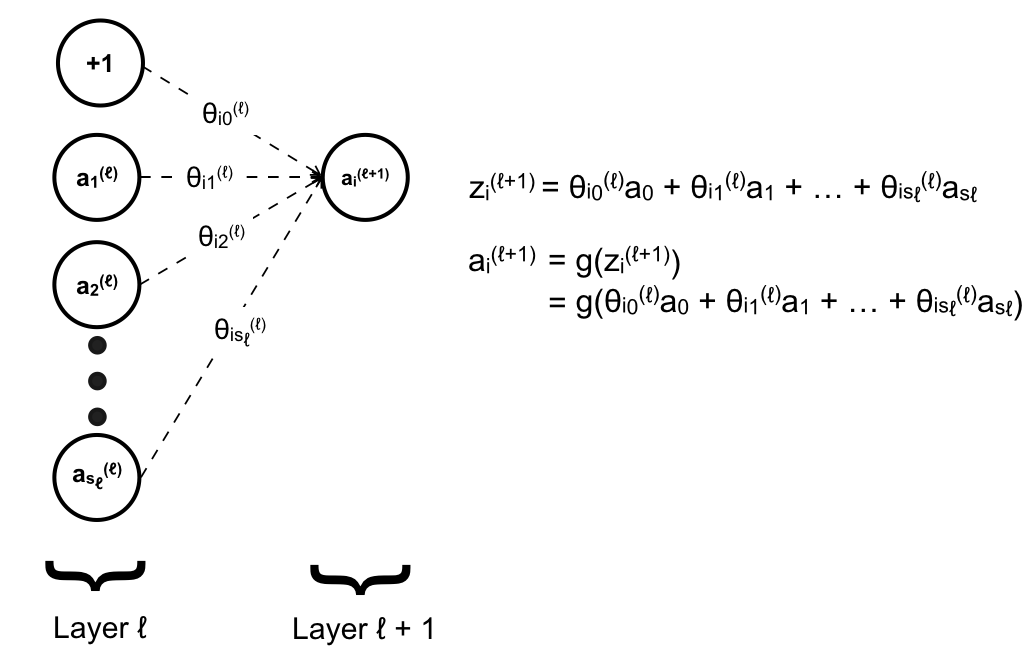
Quá trình tính toán như trên được thực hiện lần lượt từ Input Layer cho tới Output Layer sẽ cho chúng ta kết quả cuối cùng. Riêng Output Layer là layer cuối cùng nên sẽ không có matrix \(θ\) để mapping tới một layer nào tiếp theo nữa. Quá trình này được gọi là giải thuật lan truyền xuôi (Forward Propagation). Nội dung bài viết này xin được tạm dừng ở đây, trong bài viết tiếp theo chúng ta sẽ xem ANN hoạt động như thế nào qua ví dụ cụ thể.
