[ML – 08] Understanding Neural Network 2/3
Chào các bạn, trong bài viết trước chúng ta đã tìm hiểu sơ qua về ANN, đã biết về giải thuật lan truyền xuôi (Forward Propagation). Hôm nay, chúng ta tiếp tục tìm hiểu về ANN qua ví dụ cụ thể và bước đầu hiểu về cách ANN “học”.
1. Neural network – Example:
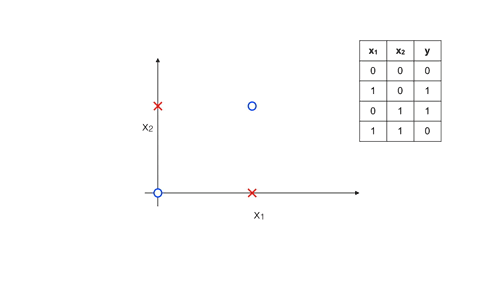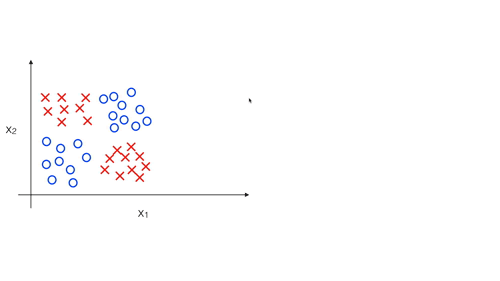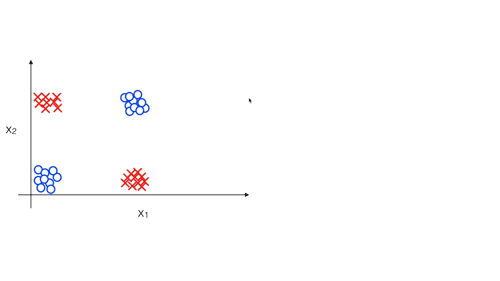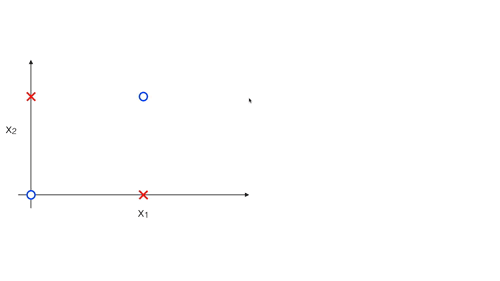
Giả sử chúng ta có một classification problem, với các feature \(x_1, x_2\) được biểu diễn như sau:
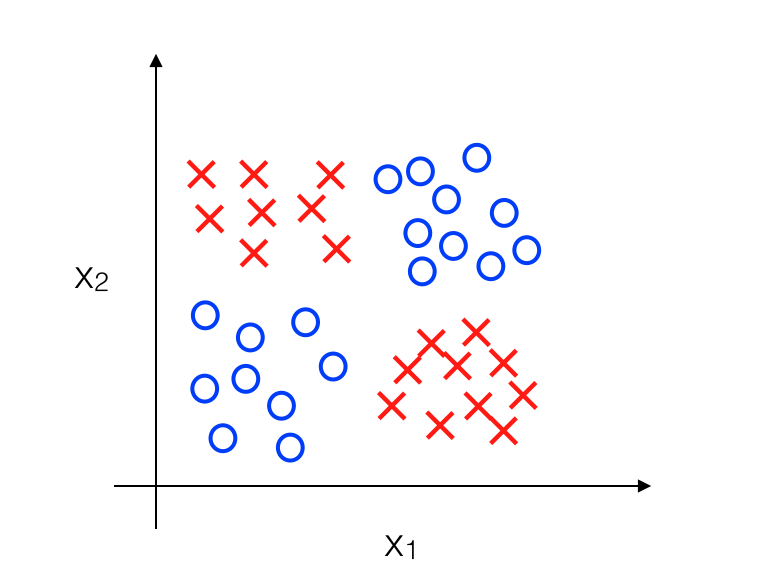
Mục tiêu của chúng ta là phải xây dựng được Decision Boundary giữa positive và negative data và nó nên có dạng như sau:
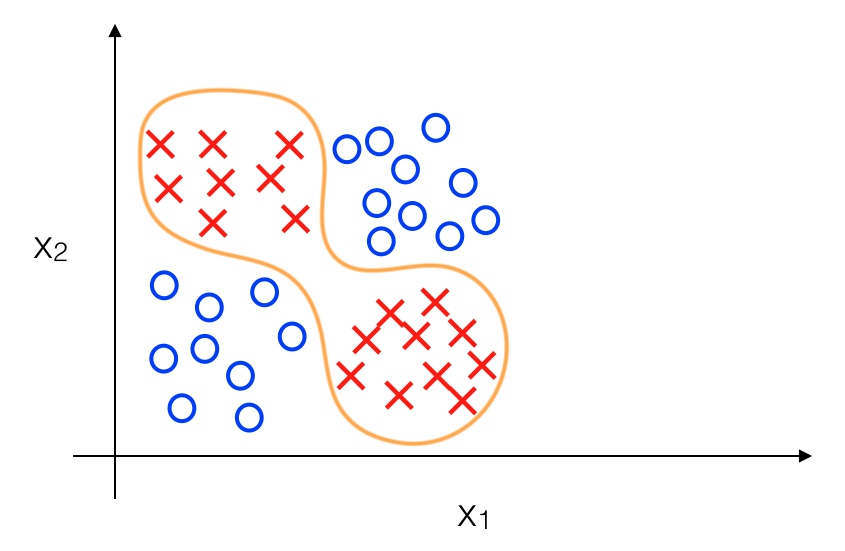
Để ý một chút ta sẽ thấy rằng dữ liệu được biểu diễn như trên được chia làm 4 nhóm, positive ở góc trái trên và phải dưới, còn negative ở góc phải trên và trái dưới. Vì vậy thực ra khi có một dữ liệu mới ta chủ yếu xác định xem dữ liệu đó thuộc nhóm nào, tương tự như việc xác định y với \(x_1, x_2\) chỉ là 0 hoặc 1 :
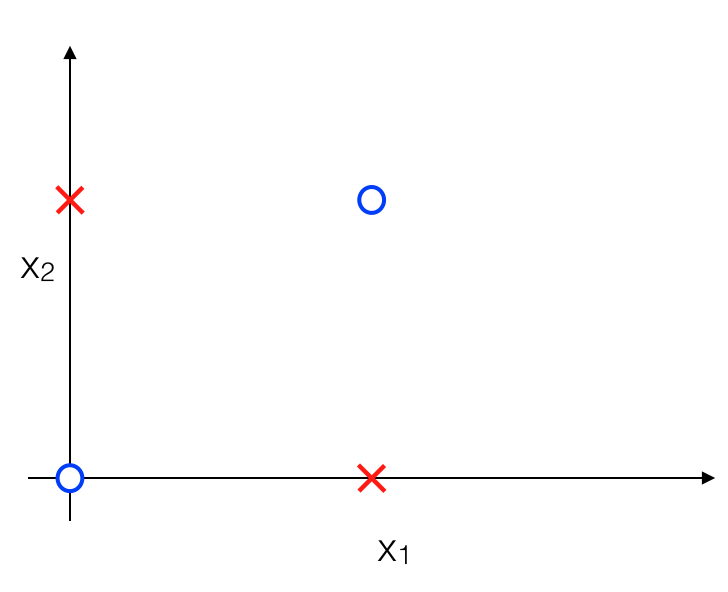
Dữ liệu trên thực chất có xu hướng tương tự bảng chân lý như sau:

Phép logic ứng với bảng chân lý trên được gọi là XNOR \(=> y = x_1 XOR x_2 = (x_1 AND x_2) OR ( (NOT x_1) AND (NOT x_2))\). Nếu như sử dụng Logistic Regression ta sẽ phải thêm những thành phần đa thức của \(x_1, x_2\) vì như Decision Boundary ở trên là đường cong nhưng nếu sử dụng ANN ta có thể không cần thêm feature nào !!! Cụ thể, tương tự như \(y = (x_1 AND x_2) OR ( (NOT x_1) AND (NOT x_2) )\) ta sẽ thiết kế ANN với các thành phần tương ứng với các phép logic trong đẳng thức.
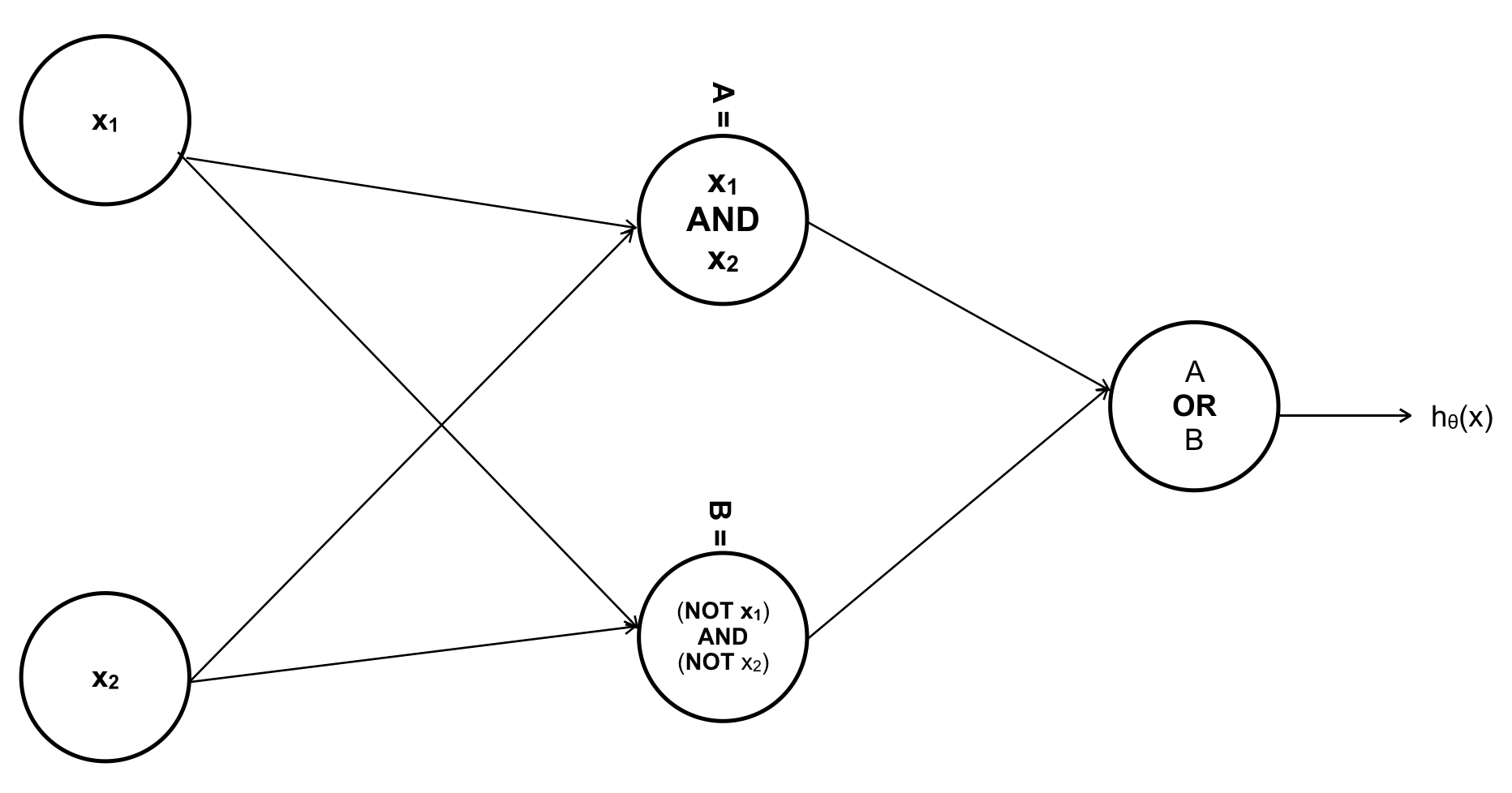
Nếu như có thêm thành phần bias, ANN sẽ như sau :
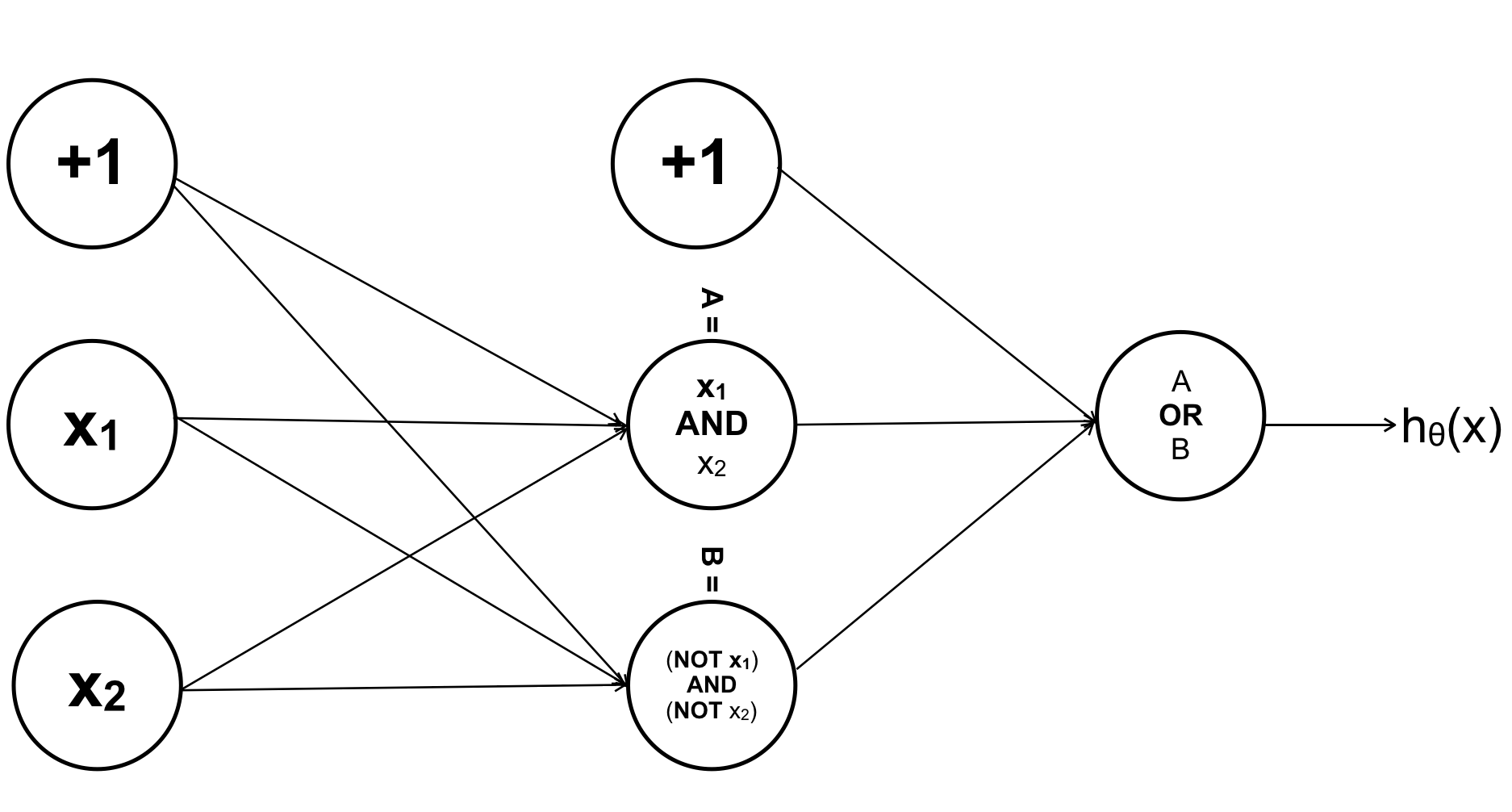
Ta đi xây dựng 3 sigmoid function, để tiết kiệm thời gian tôi sẽ đưa ra các tham số kết quả luôn:
Hàm A AND B:
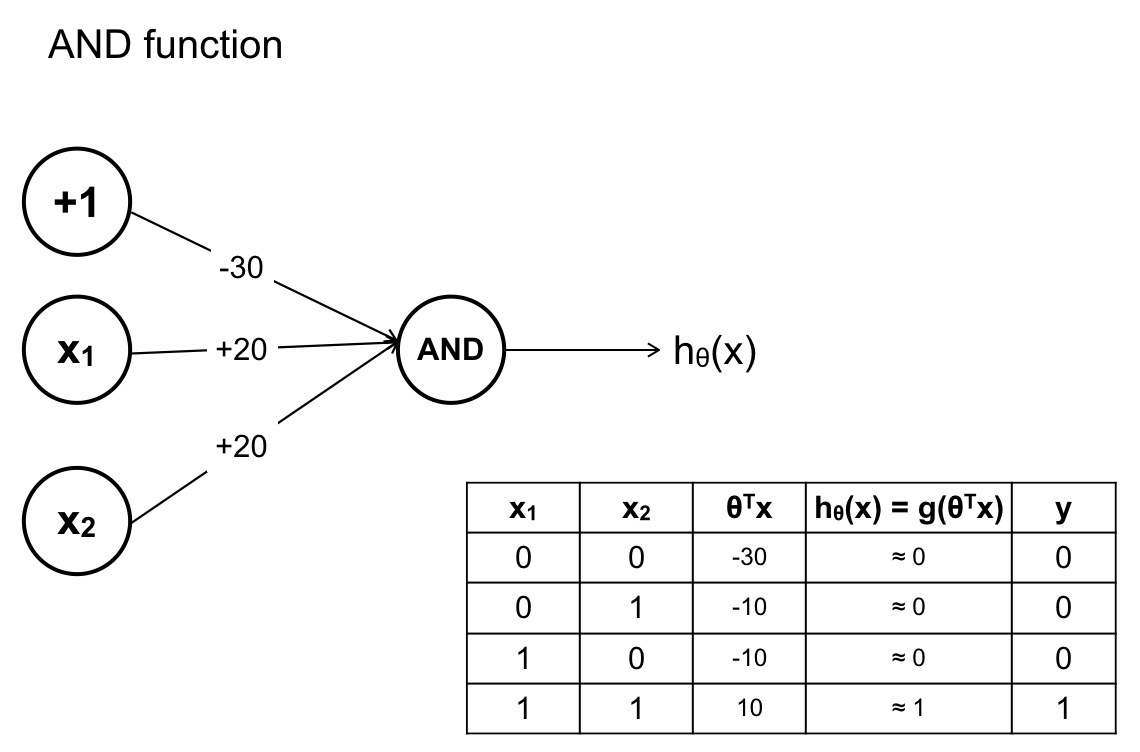
Hàm (NOT A) AND (NOT B):

Hàm A OR B:
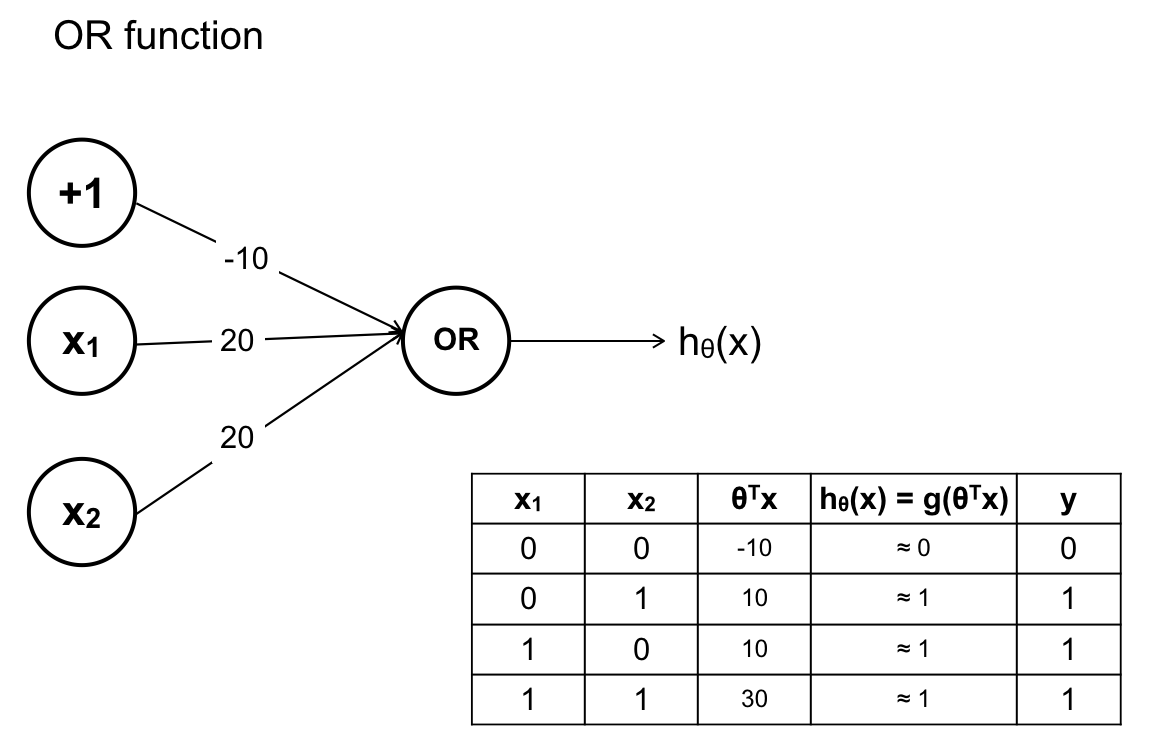
Chắp nối các hàm sigmoid trên ta sẽ có ANN giải quyết được vấn đề ban đầu.
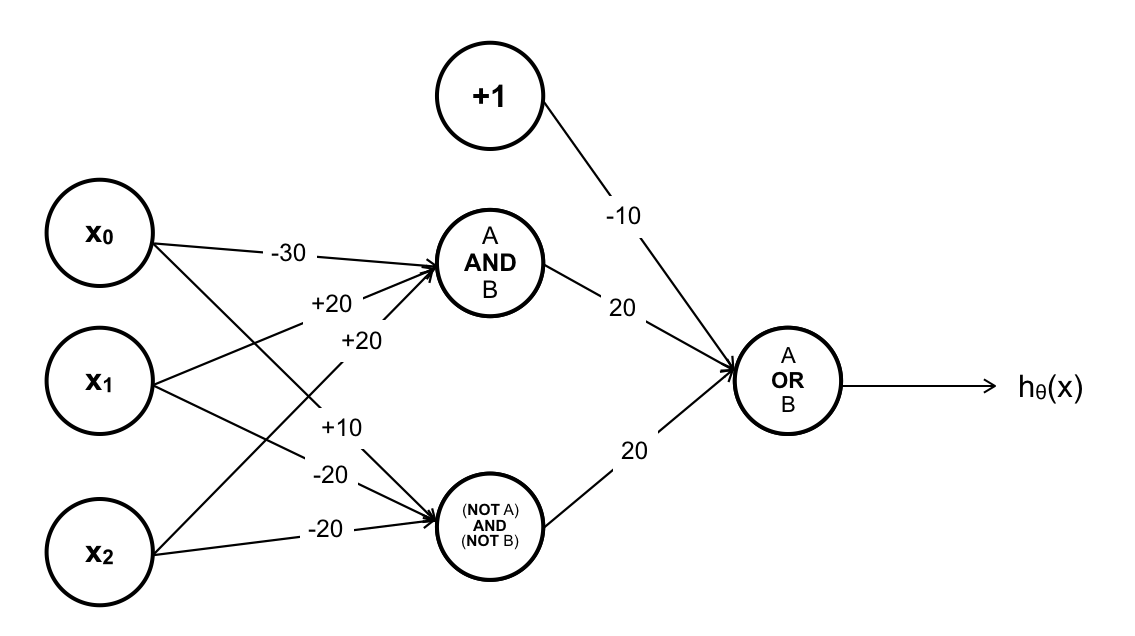
2. Neural network – Learning:
Đi tới đây chắc các bạn cũng đã hiểu ANN hoạt động như thế nào nhưng chưa biết nó “học” như thế nào ? Nếu như với Linear Regression hay Logistic Regression chúng ta đã biết về giải thuật Gradient Descent thì ANN cũng có thể học theo cách tương tự. Vấn đề ở đây là muốn áp dụng Gradient Descent ta cần biết được đạo hàm riêng tại mỗi tham số \(\theta\). Nếu để ý một chút ta sẽ thấy rằng ANN thực chất là hàm số với đầu vào là đầu ra của hàm số khác, vì thế ta hoàn toàn có thể tính được đạo hàm của \(J(\theta)\) tại mỗi tham số \(\theta\) (hàm \(J(\theta)\) được xây dựng dựa vào hàm activation trong neurons của lớp Output, trong trường hợp này nó chính là cost function của Logistic Regression). Để tính đạo hàm tại mỗi tham số \(\theta\) ta có 2 cách, ví dụ cụ thể như sau:
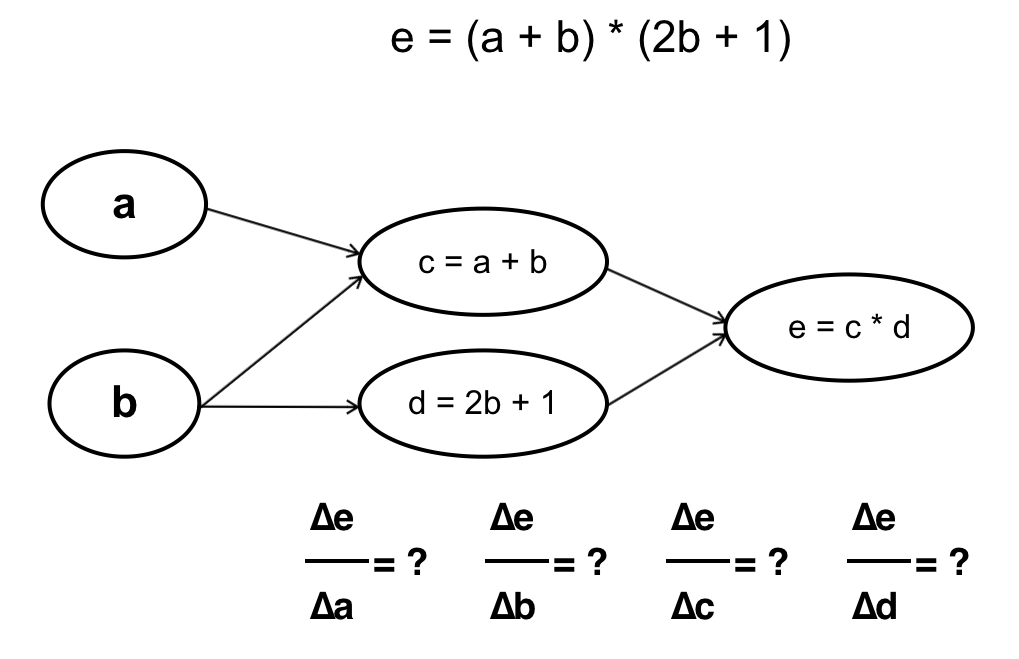
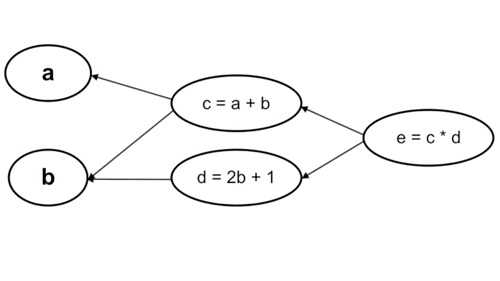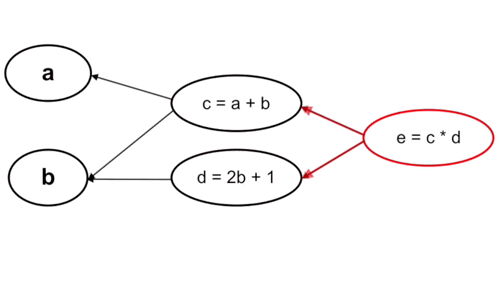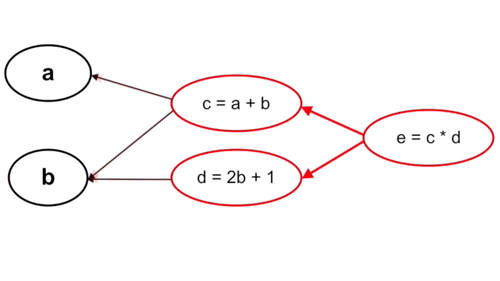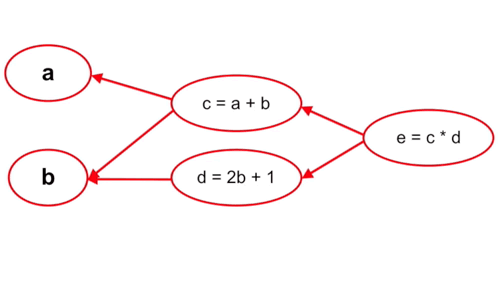
- Tính xuôi: Ta tính từ những tham số đầu tiên trong hàm số, cụ thể trong trường hợp này là từ \(a\) và \(b\). Chú ý rằng cách này với mỗi phép tính đạo hàm tại \(a\) và \(b\) ta sẽ phải đi qua bước tính \(c\) và \(d\) một lần, nghĩa là đạo hàm tại \(c\) và \(d\) sẽ được tính tận 2 lần (Vì \(y = f(g(x)) \rightarrow y’ = f’(x) * g’(x))\).
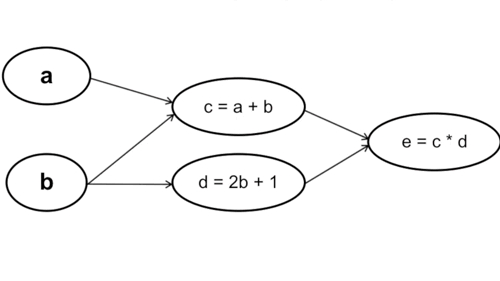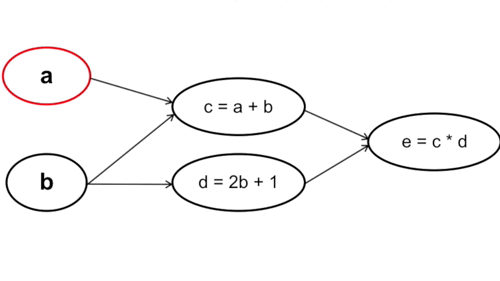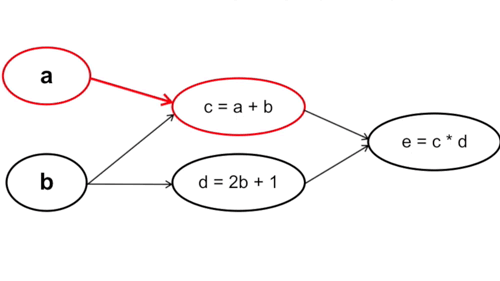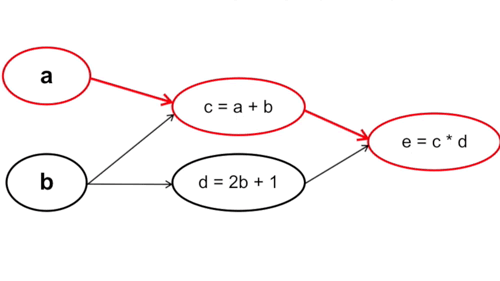
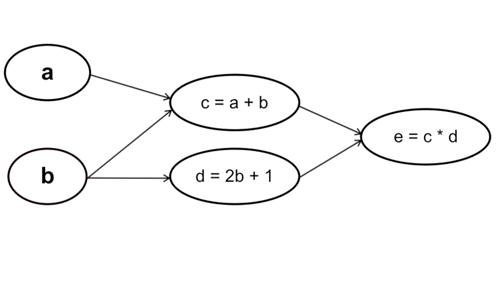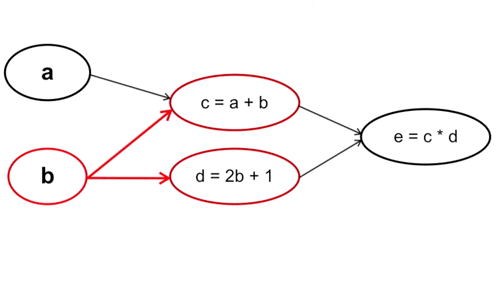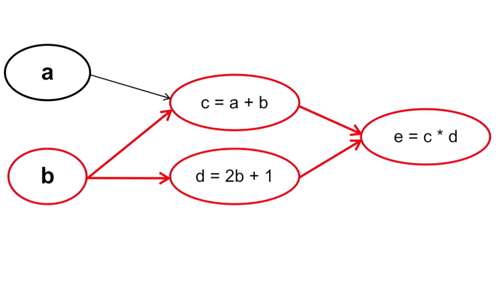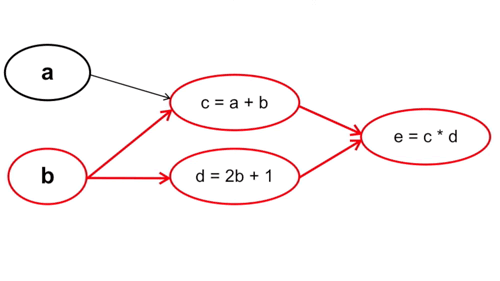
Cụ thể:
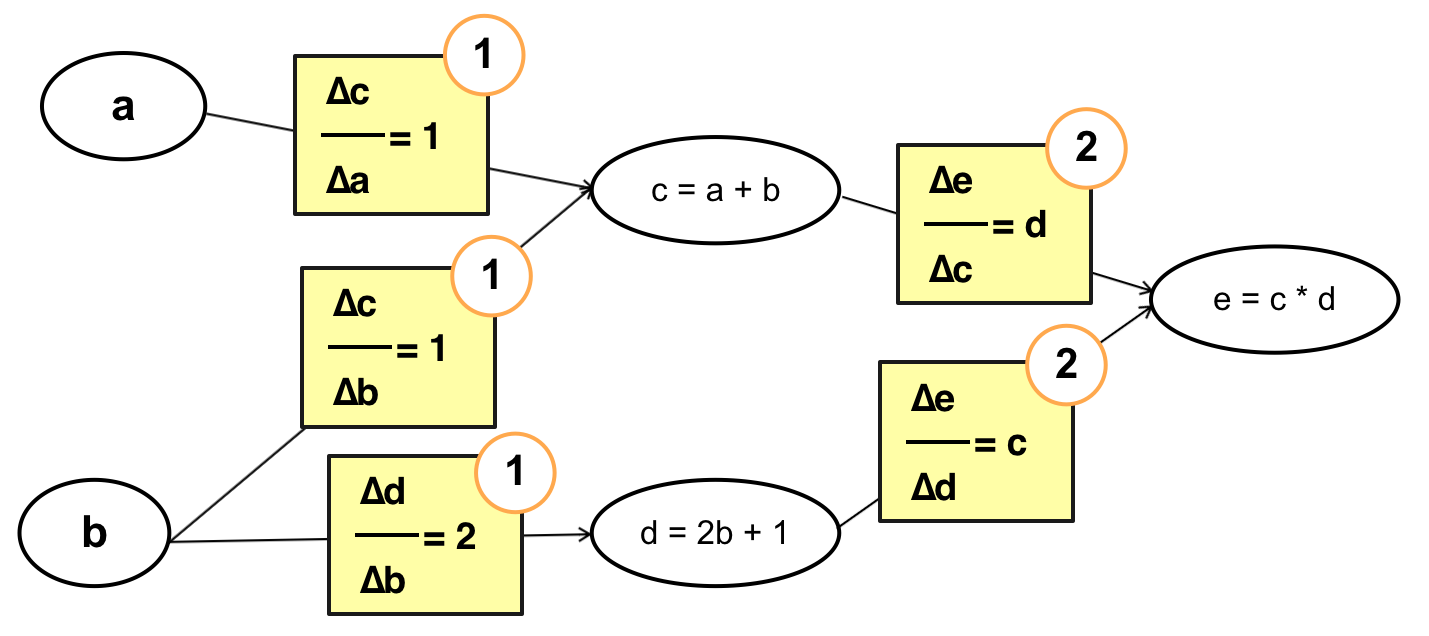
- Tính ngược:
Cách làm này thì ngược lại, ta tính từ những tham số cuối cùng trong hàm số, cụ thể trường hợp này là từ \(c\) và \(d\). Với cách tính này thì mỗi bước tính chỉ phải thực hiện một lần chứ không phải trải qua 2 lần tính \(c\) và \(d\) như cách tính xuôi.
Cụ thể:
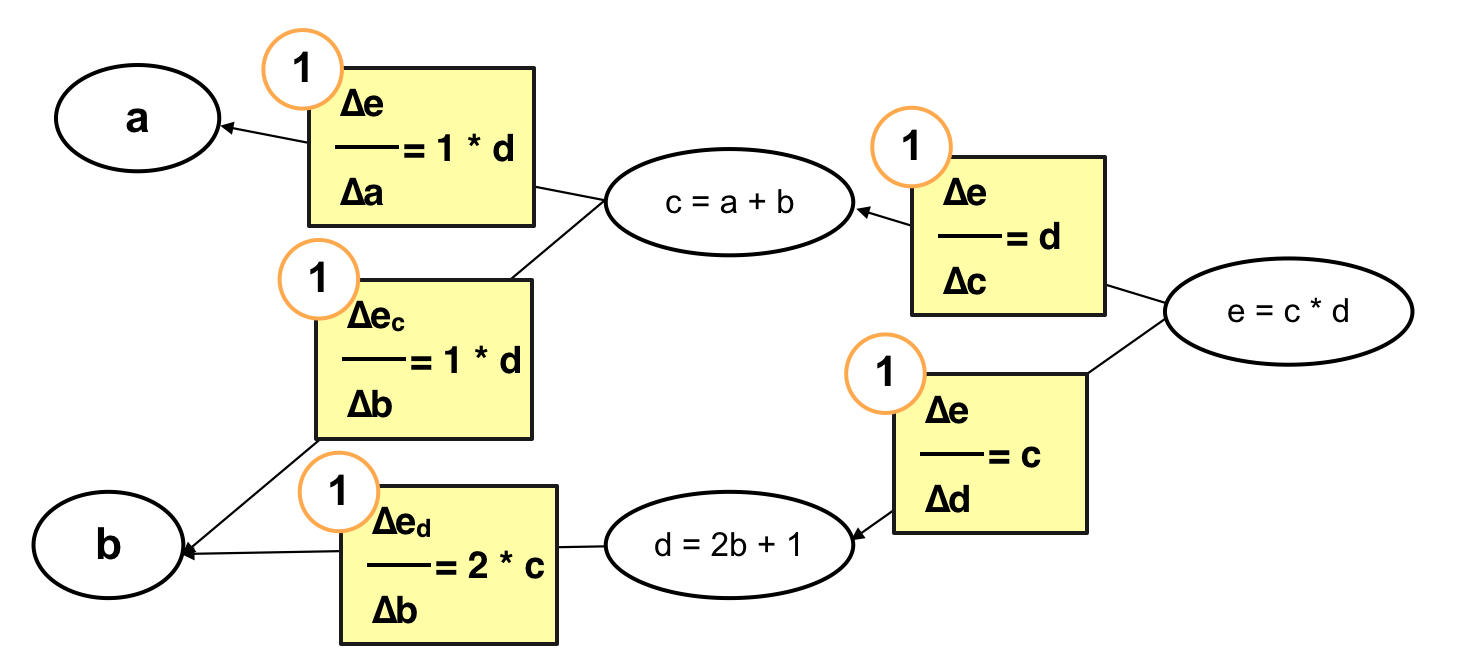
Qua 2 cách tính trên có thể thấy rằng, nếu như tính ngược ta sẽ tiết kiệm được việc tính \(c\) và \(d\) nhiều lần. Đặc biệt khi số lượng hàm số trong hàm số hay nói cách khác là số lượng neurons, số lượng layer lớn sẽ giảm thiểu được đáng kể hiệu năng bỏ ra để tính toán. Đây cũng chính là tiền đề cho giải thuật “Back Propagation” – giải thuật lan truyền ngược. Trong bài viết tiếp theo tôi sẽ đi sâu vào cụ thể hoá giải thuật này, chúng ta sẽ thấy nó chỉ phức tạp chứ không hề khó. Hẹn gặp lại các bạn trong bài viết sau!!
