[ML – 09] Understanding Neural Network 3/3
Xin chào các bạn, hôm nay chúng ta tiếp tục loạt bài về ANN. Trong bài viết trước chúng ta đã đi vào ví dụ cụ thể xem ANN vận hành như thế nào, và nó có lợi hơn so với Logistic Regression ra sao đồng thời cũng đã bước đầu tưởng tượng được ANN học như thế nào. Khi áp dụng giải thuật Gradient Descent với yêu cầu cần tính đạo hàm tại tất cả các tham số \(\theta\) hay nói cách khác là xác định xem mỗi tham số \(\theta\) ảnh hưởng tới cost function như thế nào. Ở bài trước ta đã biết 2 cách tính đạo hàm và thấy được rằng cách tính ngược đạo hàm của cost function \(J(\theta)\) tại mỗi node hay mỗi neuron sẽ giảm thiểu chi phí tính toán đi rất nhiều (khi ANN càng phức tạp). Bây giờ chúng ta sẽ xem, nếu áp dụng cụ thể, giải thuật sẽ như thế nào ?
1. Cost function:
Đối với ANN thì cost function phụ thuộc vào hàm activation của layer cuối cùng (Output Layer), mà trong trường hợp cụ thể xuyên suốt 3 bài viết về ANN này thì mọi hàm activation đều là Sigmoid Function. Vì vậy nên cost function sẽ có dạng tương tự Logistic Regression:
\[ J(\theta) = -\frac{1}{m} (\sum_{i=1}^{m}y^{(i)}log(h_{\theta}(x^{(i)})) + (1-y^{(i)})log(1 - h_{\theta}(x^{(i)}))) \]
Đối với ANN có k output hay dùng để phân loại \(\mathbf{k}\) label khác nhau thì cost function có dạng:
\[h_{\theta}(x) \in R^{k}
(h_{\theta}(x))_{k} = k^{th} output\]
\[ J(\theta) = -\frac{1}{m}[\sum_{i=1}^{m}\sum_{k=1}^{k} y_{k}^{(i)} log(h_{\theta}(x^{(i)}))_k + (1 - y^{(i)}) log(1 - (h _{\theta} (x^{(i)})) _{k})] \]
Trong đó ở đây \(\mathbf{m}\) là số lượng training example trong training set, còn \(\mathbf{k}\) là số lượng output hay số lượng label. Để đơn giản, trước tiên ta sẽ làm việc với training set chỉ có 1 training example duy nhất và mỗi layer chỉ có 1 neuron. Cost function và mạng neuron trong ví dụ hôm nay sẽ như sau:
\[J(\theta) = [ ylog(h_{\theta}(x)) + (1-y)log(1-h_{\theta}(x)) ]\]
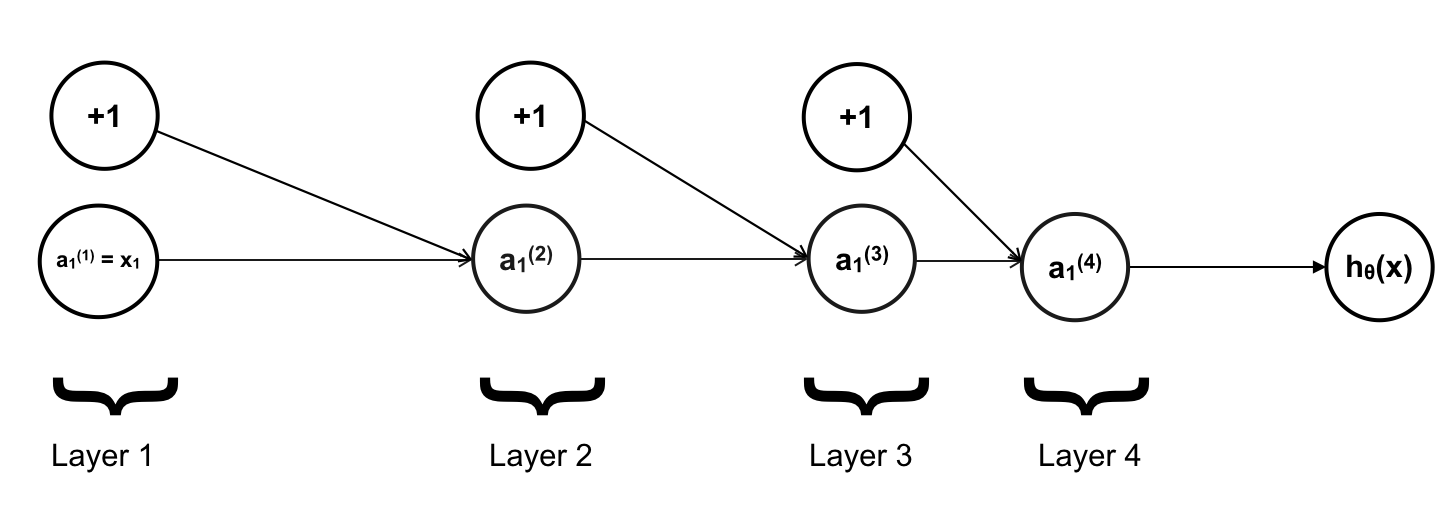
Mục tiêu của ta là tính đạo hàm tại mỗi tham số \(\mathbf{\theta}\), chẳng hạn với \(\theta_{11}^{(1)}\):
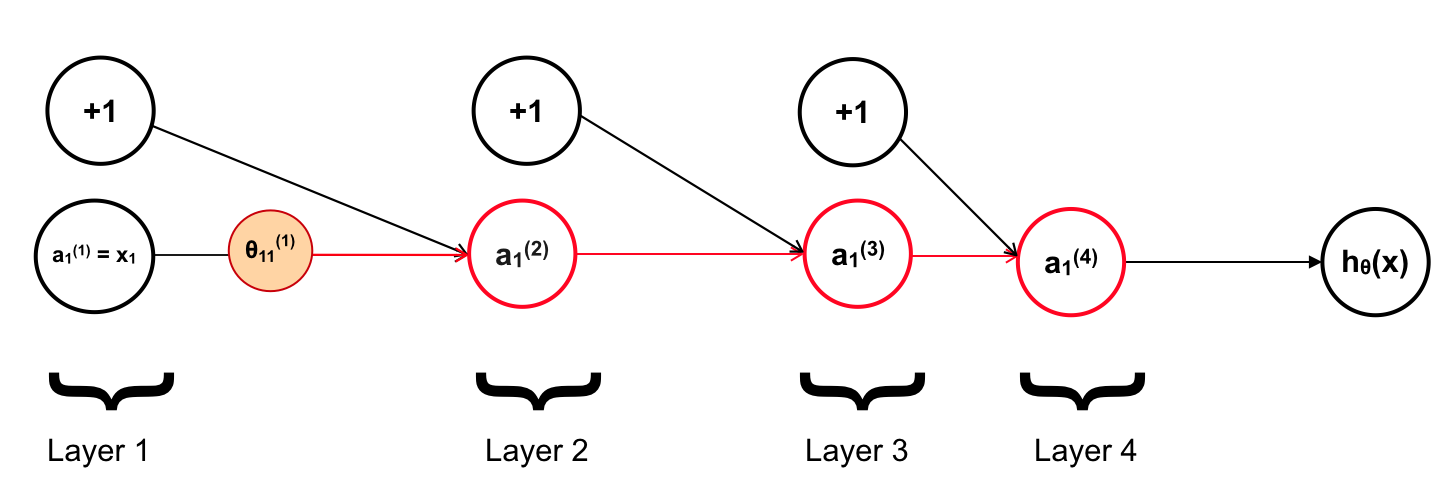
2. Back Propagation Algorithm:
Giờ chúng ta xem \(\theta_{11}^{(1)}\) ảnh hưởng tới các neuron như thế nào ? Đầu tiên là \(a_{1}^{(2)}\)
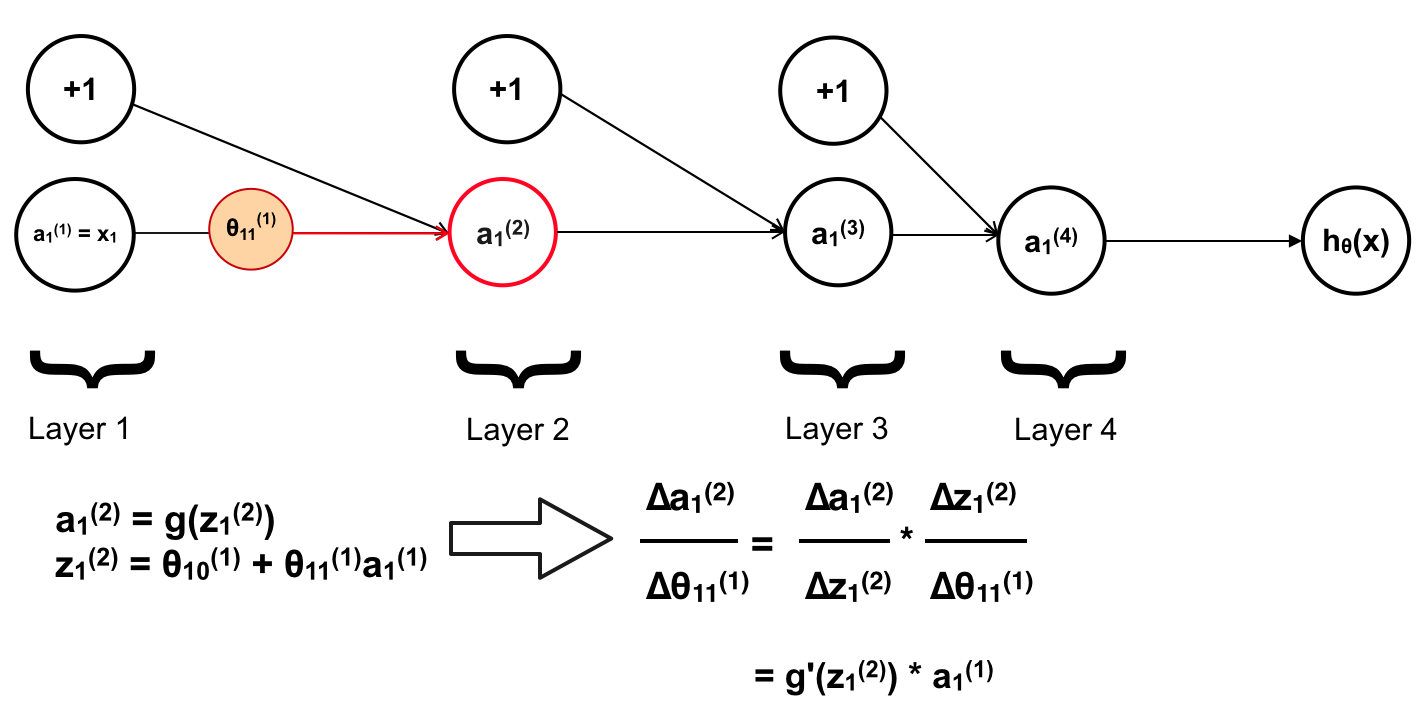
Tiếp theo là \(a_{1}^{(3)}\)
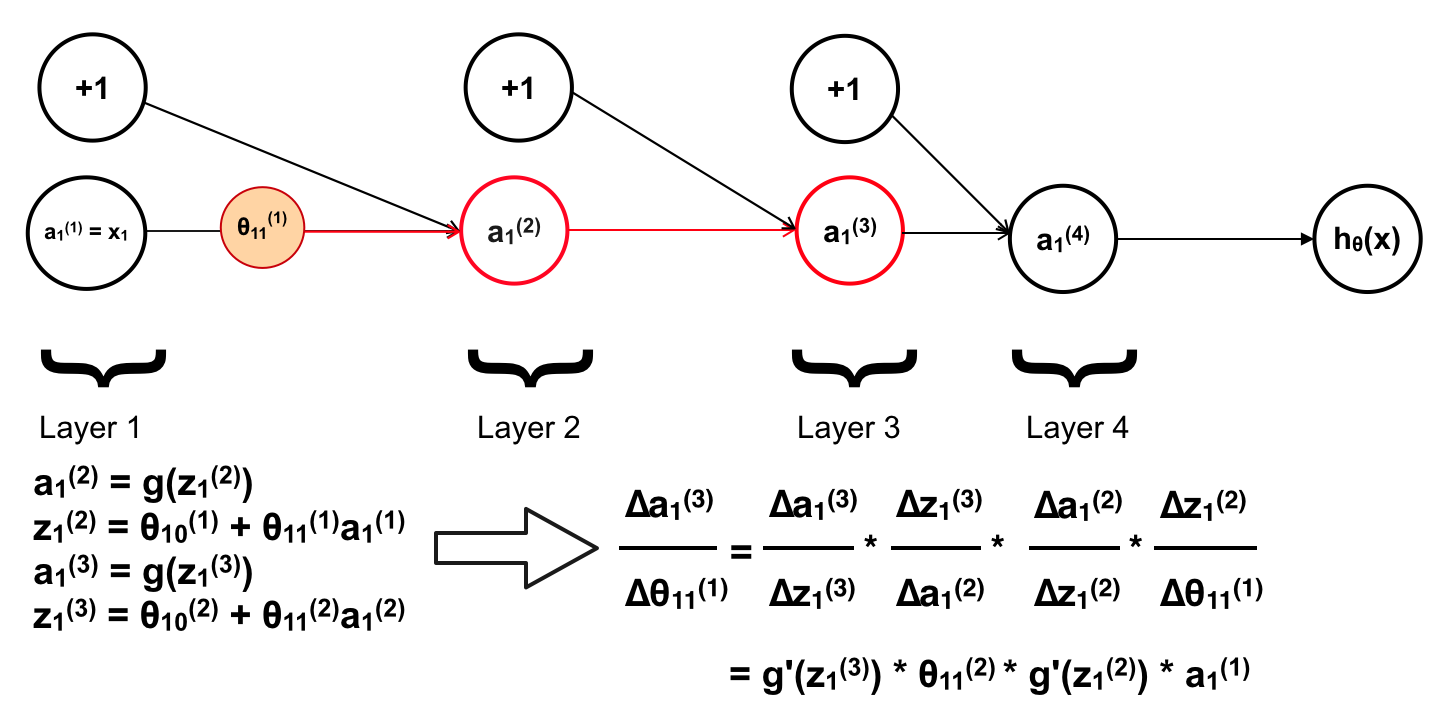
Tiếp tục với \(a_{1}^{(4)}\)
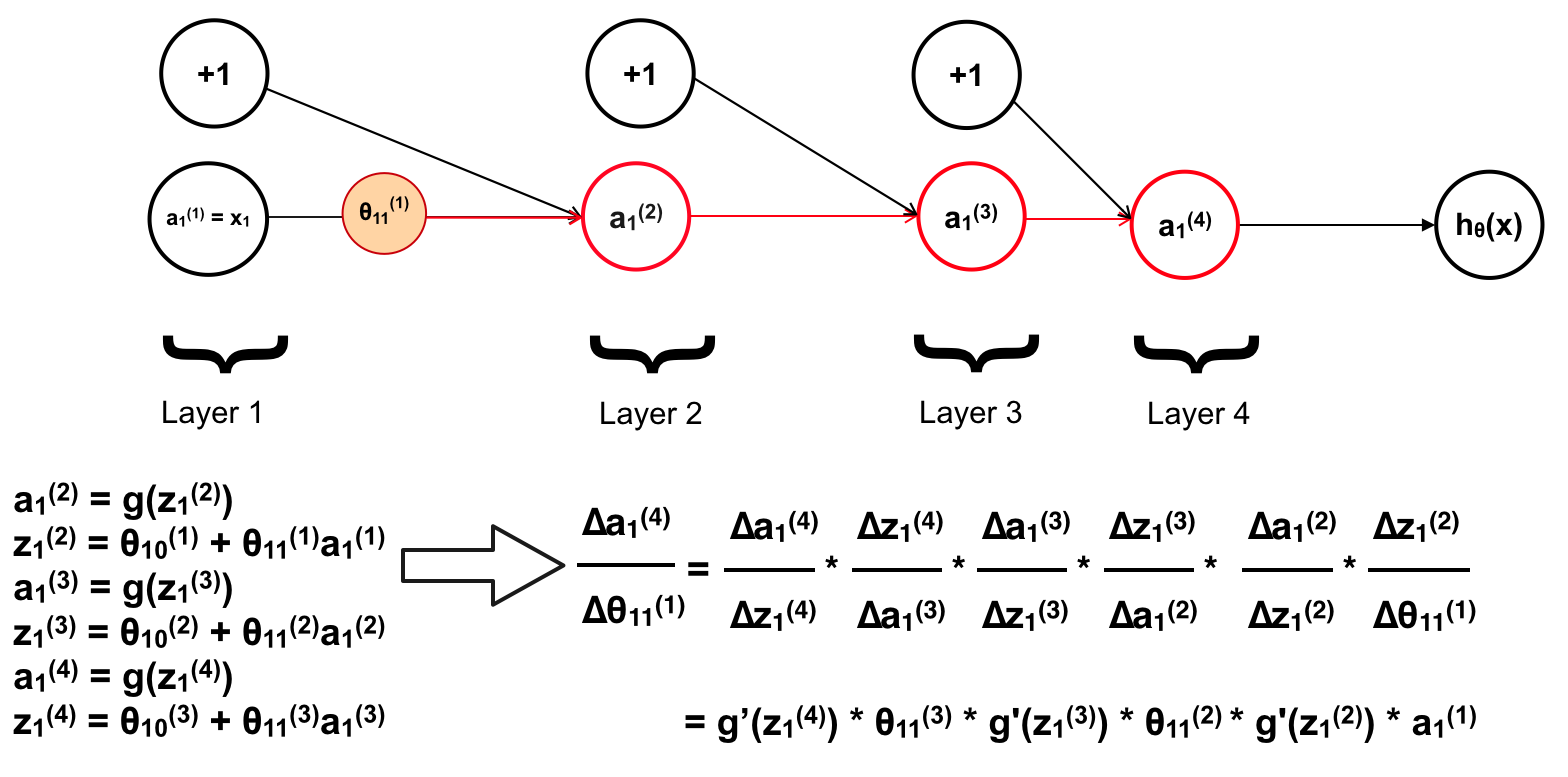
Ở đây \(a_{1}^{(4)}\) chính là \(h_{\theta}(x)\). Mà trong bài về Logistic Regression chúng ta đã tính ra được đạo hàm riêng tại mỗi \(\theta\) có dạng:
\[\\ \begin{align*} &\space \space J(\theta) = \Bigg[ y \space log \space h_\theta(x) + (1-y) \space log(1 - h_\theta(x)) \Bigg] \\ \Rightarrow & \space J'(\theta) = (h(x) - y) * \frac{\triangle z}{\triangle \theta} \space \space \space \space \space \space (z = \theta^Tx) \\ \\ \Rightarrow & \space J'(\theta) = (h(x) - y) * x_j \end{align*}\]Nên đạo hàm tại \(z_{1}^{(4)}\), hay \(z_{1}^{(4)}\) ảnh hưởng tới cost function là \(a_{1}^{(4)} – y\) (chính là \(h_{\theta}(x) – y)\). Vì khi đó đạo hàm riêng của \(J\) tại \(z_{1}^{(4)}\) sẽ có phần đạo hàm của \(z\) trên \(\theta\) bằng \(1\). Chính vì vậy ta không cần tính toán \(\theta\) ảnh hưởng tới \(a_{1}^{(4)}\) mà chỉ cần tính \(\theta\) ảnh hưởng tới \(z_{1}^{(4)}\). Ta bỏ đi phần đạo hàm trên \(a_{1}^{(4)}\) sẽ có:
\[\begin{align*} \frac{\Delta z_{1}^{4}}{\Delta \theta_{11}^{1}} & = \frac{\Delta z_1^{(4)}}{\Delta a_1^{(3)}} * \frac{\Delta a_1^{(3)}}{\Delta z_1^{(3)}} * \frac{\Delta z_1^{(3)}}{\Delta a_1^{(2)}} * \frac{\Delta a_1^{(2)}}{\Delta z_1^{(2)}} * \frac{\Delta z_1^{(2)}}{\Delta \theta _{11}^{(1)}}\\ & = \theta _{11}^{(3)} * g'(z_1^{(3)}) * \theta _{11}^{2} * g'(z_1^{(2)}) * a_1^{(1)} \end{align*}\]Nếu như ta thêm 1 feature x2 ta sẽ có kết quả tương tự khi tính đạo hàm riêng tại \(\theta_{12}^{(1)}\):
\[\begin{align*} \frac{\Delta z_{1}^{4}}{\Delta \theta_{12}^{1}} & = \frac{\Delta z_1^{(4)}}{\Delta a_1^{(3)}} * \frac{\Delta a_1^{(3)}}{\Delta z_1^{(3)}} * \frac{\Delta z_1^{(3)}}{\Delta a_1^{(2)}} * \frac{\Delta a_1^{(2)}}{\Delta z_1^{(2)}} * \frac{\Delta z_1^{(2)}}{\Delta \theta _{11}^{(1)}}\\ & = \theta _{11}^{(3)} * g'(z_1^{(3)}) * \theta _{12}^{2} * g'(z_1^{(2)}) * a_2^{(1)} \end{align*}\]Như vậy nếu như ta muốn tính đạo hàm riêng tại một \(\mathbf{\theta}\) bất kì, ta coi như ANN bắt đầu từ neuron đó và tính tương tự như trên, thì mọi \(\mathbf{\theta}\) của cùng một layer sẽ có đạo hàm riêng gần như giống nhau trừ thành phần \(a_j^{(1)}\) là neuron nó liên kết (Neuron bắt đầu, \(\theta_{ij}^{ℓ}\) liên kết từ neuron \(j\) ở layer \(ℓ\) tới neuron \(i\) ở layer \(ℓ+1\) ). Quan sát ví dụ trên sẽ thấy rất rõ với 2 feature \(x_1\) và \(x_2\). Bên cạnh đó nếu để ý một chút là các phần \(θ_{11}^{(i)} * g’(z_1^{(i)})\) lặp lại khi ta tính qua mỗi layer.
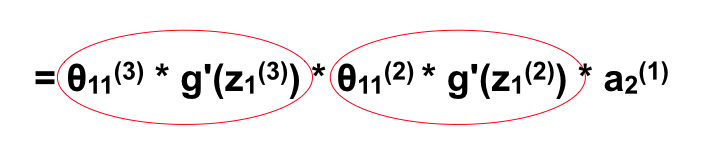
Vậy nếu ta tính ngược lại kết quả sẽ như sau:
\[\begin{align*} \frac{\Delta z_1^{(4)}}{\Delta \theta _{11}^{(1)}} & = \theta _{11}^{3} * g'(z_1^{(3)}) * \theta _{11}^{2} * g'(z_1^{(2)}) * a_1^{(1)}\\ \frac{\Delta z_1^{(3)}}{\Delta \theta _{11}^{(1)}} & = \theta _{11}^{2} * g'(z_1^{(2)}) * a_1^{(1)}\\ \frac{\Delta z_1^{(2)}}{\Delta \theta _{11}^{(1)}} & = a_1^{(1)}\\ \end{align*}\]Hay:
\[\begin{align*} \frac{\Delta z_1^{(4)}}{\Delta \theta_{11}^{(1)}} & = \frac{\Delta z_1^{(4)}}{\Delta z_{1}^{(3)}} * \frac{\Delta z_1^{(3)}}{\Delta \theta_{11}^{(1)}}\\ & = \frac{\Delta z_1^{(4)}}{\Delta a_{1}^{(3)}} * \frac{\Delta a_1^{(3)}}{\Delta z_{1}^{(3)}} * \frac{\Delta z_1^{(3)}}{\Delta \theta_{11}^{(1)}}\\ & = \theta _{11}^{(2)} * g'(z_1^{(2)}) * \frac{\Delta z_1^{(3)}}{\Delta \theta _{11}^{(1)}} \end{align*}\]Giờ chúng ta sẽ tổng quát hoá quá trình này, và tạo ra một đại lượng mới \(\mathbf{\delta} \) để tiện cho việc tính toán. \(\mathbf{\delta} \) được gọi là sai số (error) tại mỗi neuron có giá trị được tính như sau:
\[ \delta _j^{(ℓ)} = \frac{\Delta J}{\Delta z_j^{(ℓ)}}\]
Cụ thể là error của neuron thứ j trên layer \(ℓ\). Với ví dụ trên, error của neuron thứ 1 của layer 4 là
\[ \delta _j^{(4)} = \frac{\Delta J}{\Delta z_j^{(4)}} = a_1^{(4)} - y\]
tương tự với các neurons khác:
\[ \delta_1^{(3)} = \frac{\Delta J}{\Delta z_1^{(3)}} = \frac{\Delta J}{\Delta z_1^{4}} * \frac{\Delta z_1^{(4)}}{\Delta z_1^{(3)}} = \delta_1^{(4)} * \theta _{11}^{(3)} * g’(z_1^{(3)}) \]
\[ \delta_1^{(2)} = \frac{\Delta J}{\Delta z_1^{(2)}} = \frac{\Delta J}{\Delta z_1^{3}} * \frac{\Delta z_1^{(3)}}{\Delta z_1^{(2)}} = \delta_1^{(3)} * \theta _{11}^{(2)} * g’(z_1^{(2)}) \]
\(\delta _1^{(1)} = !!!\) không có sai số do đây là input
Với mỗi layer có số lượng neuron lớn hơn 1 thì sai số của neuron của một layer sẽ được tính thông qua tất cả các neuron của layer liền kế tiếp nó! (Không tính bias)
Nếu viết dưới dạng vector, layer \(ℓ\) sẽ có error là vector \(\delta(ℓ)\), còn weight hay tham số từ neuron \(j\) layer \(ℓ\) tới layer \(ℓ + 1\) sẽ là vector \(\theta _j^ℓ\), cụ thể:
\[ \delta _j^{(ℓ)} = (\theta _j^{(ℓ)})^{T}\delta ^{(ℓ + 1)} * g’(z_j^{(ℓ)}) \]
còn để tính error cho cả layer thì kết quả là: \[ \delta ^{(ℓ)} = (\theta ^{(ℓ)})^{T}\delta ^{(ℓ + 1)}\space .* \space g’(z^{(ℓ)}) \]
Trong đó tham số của tất cả neuron trong một layer không còn là một vector như trên nữa mà là một matrix như ta đã nói trong phần 1, matrix \(θ\) có kích thước \((s_{ℓ+1})\)x\((s_ℓ + 1)\) và \(\delta^{ℓ+1}\) là vector \(s_ℓ+1\) chiều. Bên cạnh đó phép toán ” \(. *\) ” là lấy từng phần tử của vector thu được sau khi nhân matrix \(θ\) và vector \(\delta\) với các phần tử tương ứng của vector \(g’(z^{(ℓ)})\) (Đây là phép toán có trong MathLab, nếu các bạn có kinh nghiệm về nó thì chắc hẳn sẽ rất quen thuộc). Và giờ để tính đạo hàm cho các \(θ\), ta chỉ cần:
\[ \frac{\Delta J}{\Delta \theta_{ij}^{(ℓ)}} = \frac{\Delta J}{\Delta z_i^{(ℓ + 1)}} * \frac{\Delta z_i^{(ℓ + 1)}}{\Delta \theta_{ij}^{(ℓ)}} = \delta^{(ℓ + 1)} * a_j^{(ℓ)}\]
Đến đây thì chúng ta đã hiểu được cách tính đạo hàm riêng tại các tham số \(\theta\). Với việc tính toán \(\delta\) ngược từ output layer giúp giảm thiểu chi phí tính toán và thuận tiện trong việc chuyển đổi tương ứng sang đạo hàm riêng của \(\theta\). Vậy là các bạn đã nắm được giải thuật Back Propagation, với đạo hàm riêng thu được, áp dụng vào giải thuật Gradient Descent ta sẽ tối ưu hoá được cost function và ANN đã học thành công 🙂
