[ML – 11] Machine Learning Diagnostic 1/2
Xin chào các bạn, rất vui được gặp lại các bạn trong bài viết thứ 11 trong loạt bài về Machine Learning. Trong 10 bài viết trước chúng ta đã tìm hiểu được khá nhiều kĩ thuật như các giải thuật, mô hình, hay phương pháp xử lý khi gặp vấn đề về Underfitting và Overfitting. Hôm nay, ta sẽ cùng nhau tìm hiểu làm thế nào để xác định mô hình hay giải thuật chúng ta đang phát triển gặp phải vấn đề và cách giải quyết chúng.
1. When debugging is necessary and what to try ?
Việc tối quan trọng sau khi cài đặt mô hình, ta cần phải xác định xem mô hình hay giải thuật đó có vấn đề không ? Với vấn đề gặp phải, ta lựa chọn mô hình phù hợp (như Logistic Regression cho Classification Problem và Linear Regression cho Regression Problem). Cố gắng cài đặt và huấn luyện máy với lượng dữ liệu hiện có, kế tiếp ta đem kết quả training đi thử nghiệm với thực tế vì nếu như ta đem dữ liệu đã training để test, có thể kết quả sẽ vẫn khả quan. Lúc này nếu như lúc này kết quả thu được sai lệch quá nhiều, tới mức không thể chấp nhận được. (Như thế nào là không chấp nhận được tuỳ thuộc vào yêu cầu của dự án). Trong trường hợp đó, những giải pháp sau có thể có ích:
- Thêm dữ liệu vào tập training.
- Giảm số lượng feature.
- Tăng số lượng feature.
- Thêm thành phần đa thức.
- Thay thế toàn bộ các feature, mới hơn, tốt hơn. (Nếu như bạn hiểu rất rõ vấn đề của mình)
- Tăng giảm 𝝺. (Regularization)
- Thay đổi mô hình, giải thuật.
Mặc dù ta có những giải pháp như trên, nhưng nếu không lựa chọn một cách phù hợp có thể khiến ta mất thêm nhiều tháng trời. Chẳng hạn mô hình đã đạt độ chính xác giới hạn, dù có cố gắng thêm nhiều data, kết quả cũng không tốt hơn. (Chẳng hạn trong nhận diện chữ viết tay Softmax Regression chỉ có thể đạt độ chính xác quanh 90%, nên muốn mô hình tốt hơn ta có thể sử dụng CNN – Convolution Neuron Network).
2. Evaluating a hypothesis:
Để đánh giá hàm hypothesis một cách khách quan, ta cần một tập dữ liệu độc lập với tập training. Tuy nhiên thay vì thu thập dữ liệu mới sau quá trình học với tất cả dữ liệu ta có trước đó, ta chia tập dữ liệu ban đầu thành 2 phần:
- Data Training set (tập dữ liệu sử dụng để học, thường chiếm 70%)
- Data Test set (tập dữ liệu sử dụng để test, thường chiếm 30%)
Để đánh giá sai số của hàm hypothesis sau quá trình học trên tập dữ liệu kiểm thử, ta sử dụng cost function giống như trên tập training, riêng với Classification Problem, cost function được xây dựng dựa trên xác suất xảy ra của các cặp dữ liệu trong tập training nên ta sẽ xử lý khác một chút.
-
Với Regression Problem, tương tự như trên tập training (chẳng hạn trong mô hình Linear Regression với Least Square): \[ J _{test} (\theta) = \frac {1} {2m _{test}} \sum _{i=1} ^{m _{test}} (h _{\theta} ( x _{test} ^{(i)} ) - y _{test} ^{(i)}) ^{2} \]
-
Với Classificationn Problem, sai số là trung bình số lần mô hình dự đoán sai:
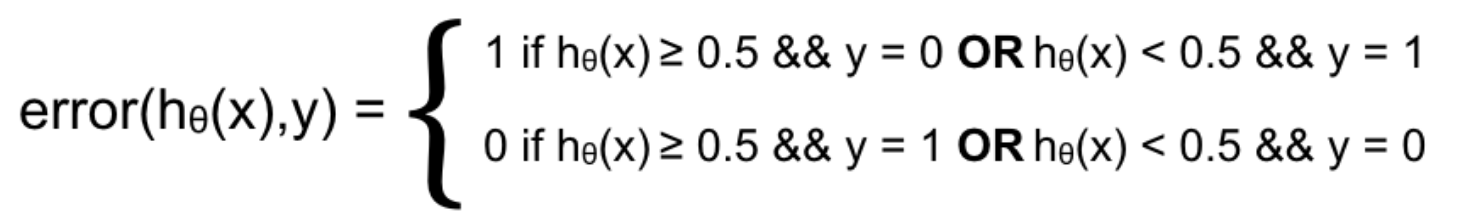
\[ J _{test} (\theta) = \frac{1}{m _{test}} \sum _{i=1} ^{m _{test}} error( h _{\theta} (x _{test} ^{(i)}), y _{test} )\]
Đây là kĩ thuật cơ bản để kiểm tra xem hàm hypothesis có tốt hay không. Nếu không tốt, ở tập test, sai số sẽ rất lớn.
3. Model selection & training validation test sets:
Khi mô hình không đủ phức tạp để mô tả được xu hướng của dữ liệu, chúng ta có thể sẽ cần tăng bậc cho x (nói cách khác là thêm các thành phần \(x^2, x^3\) … vào các feature x). Càng nâng bậc của x ta càng có mô hình fit dữ liệu trong tập training tốt hơn, tuy nhiên có thể khiến cho mô hình rơi vào tình trạng Overfitting. Dù có Regularization, ta cũng vẫn chưa biết nên chọn 𝝺 cho phù hợp. Vậy nên tăng bậc của x và chọn 𝝺 như thế nào cho phù hợp ? Ta lấy ví dụ với Linear Regression. Giả sử ta nâng x lên tới bậc 10 đã cho giá trị của cost function trên tập training rất nhỏ.
Với mỗi bậc ta lựa chọn, số lượng và giá trị các tham số \( \theta \) cũng khác. Tính sai số trên tập kiểm tra với các mô hình khác nhau ta thu được :

Một cách logic, ta sẽ lựa chọn mô hình có sai số trên tập kiểm thử nhỏ nhất. Chẳng hạn với bậc = 3, ta thu được sai số nhỏ nhất trên tập test. Đúng ra lúc này ta đem mô hình thu được đi ứng dụng phải có kết quả tốt, nhưng bằng cách nào đó, dữ liệu thực tế lại không được dự đoán tốt. Tại sao lại như vậy, rõ ràng chúng ta đã tránh để mô hình test trên tập training, nhưng khi lựa chọn bậc tốt nhất với tập test, vô tình ta đã chọn mô hình dự đoán tốt chỉ trên tập test. Một hình thức ta cho máy học trên tập test, như vậy mô hình này vẫn chưa tốt. Có lẽ ta cần một phương pháp kiểm tra hàm hypothesis tốt hơn. Thay vì chia tập dữ liệu ta có thành 2 phần, giờ ta chia chúng thành 3 phần:
-
- Training set (Dùng cho quá trình học, thường chiếm khoảng 60% với (m_{train}) bộ training data)
-
- Cross validation set (CV – Dùng thay thế cho tập test ở trên, để đánh giá khách quan hơn cho quá trình học, thường chiếm khoảng 20% với \(m_{cv}\) bộ dữ liệu)
-
- Test set (Chỉ dùng với mục đích test cuối cùng, không dùng để lựa chọn mô hình, thường chiếm khoảng 20% với \(m_{test}\) bộ dữ liệu). Cách tính sai số cho hàm hypothesis trên từng phần dữ liệu ở trên là như nhau:
\[ J _{train} (\theta) = \frac{1}{2m _{train}} \sum _{i=1} ^{m _{train}} (h _{\theta} ( x _{train} ^{(i)} ) - y _{train} ^{(i)}) ^{2} \]
\[ J _{cv} (\theta) = \frac{1}{2m _{cv}} \sum _{i=1} ^{m _{cv}} (h _{\theta} ( x _{cv} ^{(i)} ) - y _{cv} ^{(i)}) ^{2} \]
\[ J _{test} (\theta) = \frac{1}{2m _{test}} \sum _{i=1} ^{m _{test}} (h _{\theta} ( x _{test} ^{(i)} ) - y _{test} ^{(i)}) ^{2} \]
Đến đây, sau khi cho máy học trên từng mô hình, ta tính sai số cho các mô hình. Làm tương tự như trên, test hàm hypothesis với CV set và lựa chọn hàm hypothesis với sai số trên tập CV là nhỏ nhất. Sau đó ta test lại với test set. Việc làm như trên để tránh hàm hypothesis bị bias (underfitting problem). Tuy nhiên hiện nay vẫn có nhiều người bỏ qua việc tạo tập CV, mà chỉ phụ thuộc vào tập test nhưng vẫn đạt được kết quả tốt (thường là vì số lượng dữ liệu test lớn nên vẫn mô tả được xu thế của dữ liệu chung). Bản thân tôi khuyến nghị các bạn nên chia tập dữ liệu thành 3 phần như trên.
4. Diagnosis – bias & variance:
Kết quả thu được từ hàm hypothesis trên tập training, CV hay test không tốt đều bởi vì một trong hai vấn đề ta đã nói trong bài trước :
- High bias: under fitting problem
- High variance: over fitting problem
Underfitting: \(d = 1\)

Overfitting:
Khi bậc của model tăng, ta sẽ giảm thiểu được khả năng vướng vào High bias nhưng dễ vướng vào High variance. Với \(d\) là bậc của model như đã định nghĩa ở trên, ta vẽ đồ thị xem sai số trên tập training và CV thay đổi như thế nào khi \(d\) thay đổi.
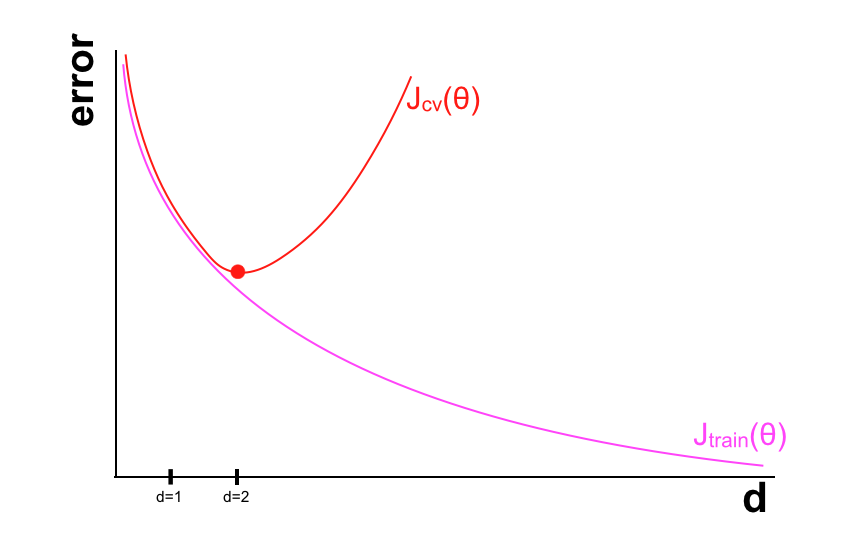
Như trên đồ thị, tại điểm \(d = 2\) thì giá trị của \(J _{cv}\) là nhỏ nhất. Với \(d\) quá nhỏ, ta sẽ vướng vào high bias problem (sai số trên cả tập training và CV đều lớn), còn với \(d\) quá lớn sẽ bị high variance problem (sai số trên tập training nhỏ nhưng trên tập CV lại lớn). Trong phần tiếp theo chúng ta sẽ tiếp tục tìm hiểu cách để lựa chọn \( \lambda \) cho phần Regularization. Cảm ơn các bạn đã theo dõi và hẹn gặp lại trong bài viết tiếp theo.
