[ML – 12] Machine Learning Diagnostic 2/2
Tiếp nối nội dung của bài 11, trong bài này ta sẽ tìm hiểu cách lựa chọn \(\lambda\) cho Regularization, đồng thời quan sát một chút quá trình learning của mô hình.
5. Regularization & bias/variance:
Tình trạng bias và variance sẽ thay đổi như thế nào khi ta tác động vào phần Regularization? Tiếp tục trở lại với ví dụ trong bài trước, trong mô hình Linear Regression với số lượng feature \(x = 1\), bậc mô hình \(d = 4\):
\[ h _{\theta} (x) = \theta _{0} + \theta _{1} x ^{1} + \theta _{2} x ^{2} + \theta _{3} x ^{3} + \theta _{4} x ^{4} \]
\[ J(\theta) = \frac{1}{2m} \sum _{i=1} ^{m} (h _{\theta} (x ^{(i)}) - y ^{(i)}) ^{2} + \frac{\lambda}{2m} \sum _{j=1} ^{4} \theta _{j} ^{2} \]
– Nếu \(\mathbf{\lambda} \) quá lớn: giá trị của tất cả \(θ\) ngoại trừ \(θ_0\) đều giảm mạnh, xấp xỉ về 0. Khi đó giá trị của hàm hypothesis chỉ còn phụ thuộc vào \(θ_0\) -> Hight bias -> Underfitting ngay trong tập training. Chẳng hạn \(\lambda\) = 100000, \(\theta_1 ≈ 0, \theta _2 \approx 0 … h _{\theta} (x) \approx \theta_0 \)
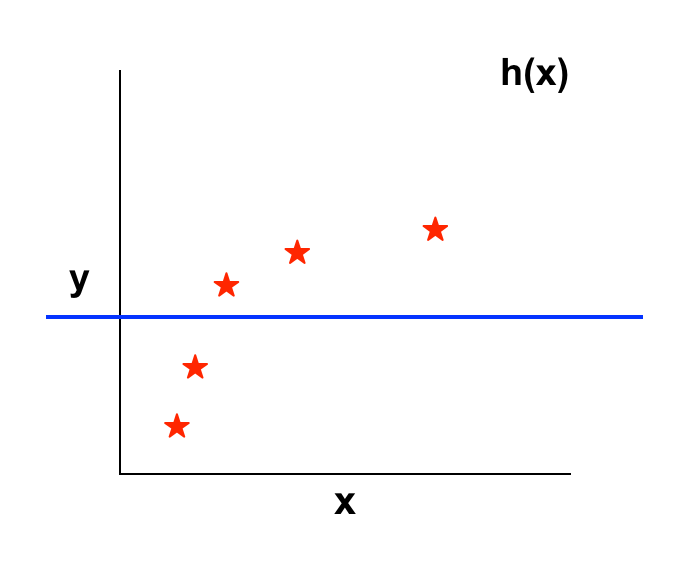
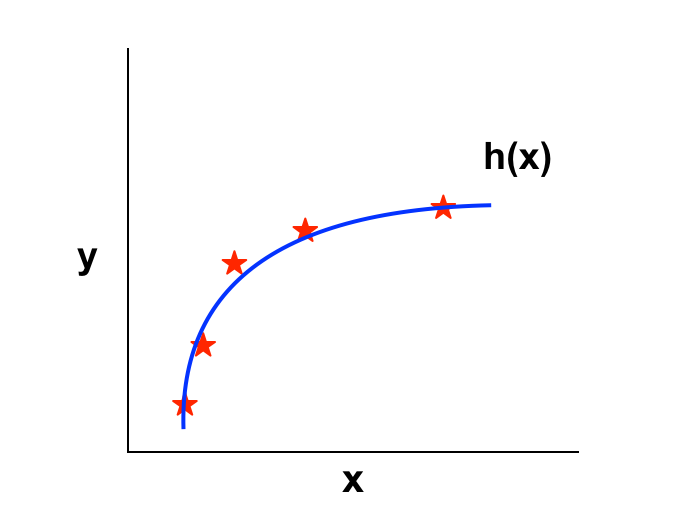
- Nếu \(\lambda\) phù hợp: Đây là giá trị \(\lambda\) ta mong muốn tìm kiếm.
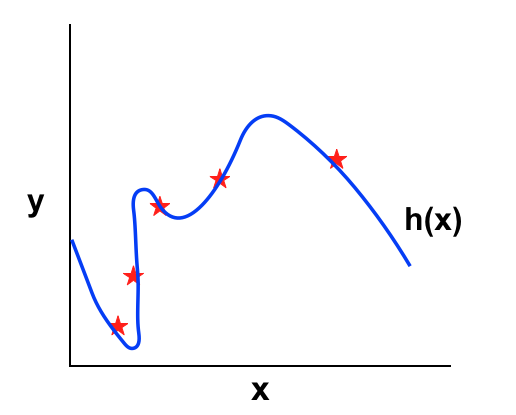
- Nếu \(\lambda\) nhỏ: xấp xỉ bằng 0, khiến cho phần Regularization nhỏ, gần với 0 hay nói cách khác là bỏ qua Regularization, khi bậc đẩy lên cao mô hình sẽ vướng vào High variance -> Overfitting
Vấn đề bây giờ là giá trị \(\lambda\) như thế nào thì được gọi là phù hợp, bản thân \(\lambda\) là số thực \(> 0\) nên nó có thể là bất cứ giá trị dương nào, dù ta có một khoảng giới hạn nhất định (chẳng hạn \(10 < \lambda < 100\)) ta cũng không thể xác định được giá trị chính xác của \(\lambda\). Chính vì vậy ta chỉ có thể xác định \(\lambda\) thông qua việc lựa chọn những giá trị rời rạc, nhưng số lượng giá trị này sẽ khá lớn nên ta sẽ tìm cách để thực hiện việc này một cách tự động. Chẳng hạn: Ta xác định được \(\lambda\) nằm trong khoảng \([0 \space ; \space 10]\) (Ở \(\lambda = 0\), mô hình bị Overfitting còn ở \(\lambda = 10\), mô hình bị Underfitting – cách kiểm tra Overfitting và Underfitting chúng ta đã đề cập đến trong các bài trước). Ta xác định model trên những giá trị của λ như sau:
- model(1): \(\lambda\) = 0
- model(2): \(\lambda\) = 0.1
- model(3): \(\lambda\) = 0.2
- model(4): \(\lambda\) = 0.4
- model(5): \(\lambda\) = 0.8
- …
- model(k): \(\lambda\) = 10
Model(k) sẽ có \(λk = 2λk-1\) của model(k-1). Vì 0 * 2 = 0 nên ta tăng \(\lambda\) của model(2) lên 0.1 Lần lượt cho máy học với \(\lambda\) tương ứng, ta thu được k bộ tham số \(\theta\) tương ứng với k model. Sau đó ta tính sai số trên tập CV của mỗi model và lựa chọn model có sai số thấp nhất, chẳng hạn \(λp\). Cuối cùng là test trên tập test để đảm bảo kết quả mang tính tổng quát. Nếu bạn muốn tìm kiếm \(\lambda\) chính xác hơn, hãy tiếp tục chia nhỏ khoảng giá trị \([λp-1 ; λp+1]\) và làm tương tự như trên. Chỉ với chút ít lập trình ta sẽ biến công việc trên thành tự động, tuy nhiên nếu cố tìm \(\lambda\) quá chính xác có thể sẽ khiến bạn đổ nhiều thời gian cho việc chờ đợi quá trình học của máy. Bên cạnh đó ta cũng có thể đưa \(\lambda\) và sai số trên tập training, tập CV để có cái nhìn trực quan:
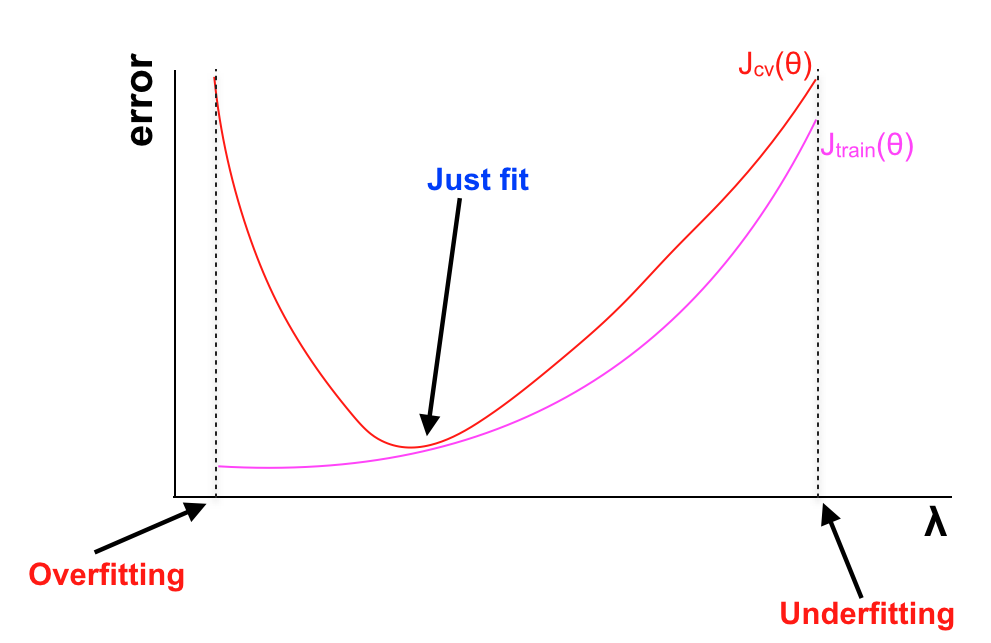
6. Learning curves:
Giờ chúng ta sẽ đi quan sát Learning curves để thấy được số lượng dữ liệu training ảnh hướng tới kết quả học của máy như thế nào ? Ta đưa giá trị của \(J_{train}\), \(J_{cv}\) và số lượng bộ dữ liệu training \(m\) vào đồ thị để quan sát xem \(m\) ảnh hưởng tới cost function \(J\) trên các tập dữ liệu ra sao:
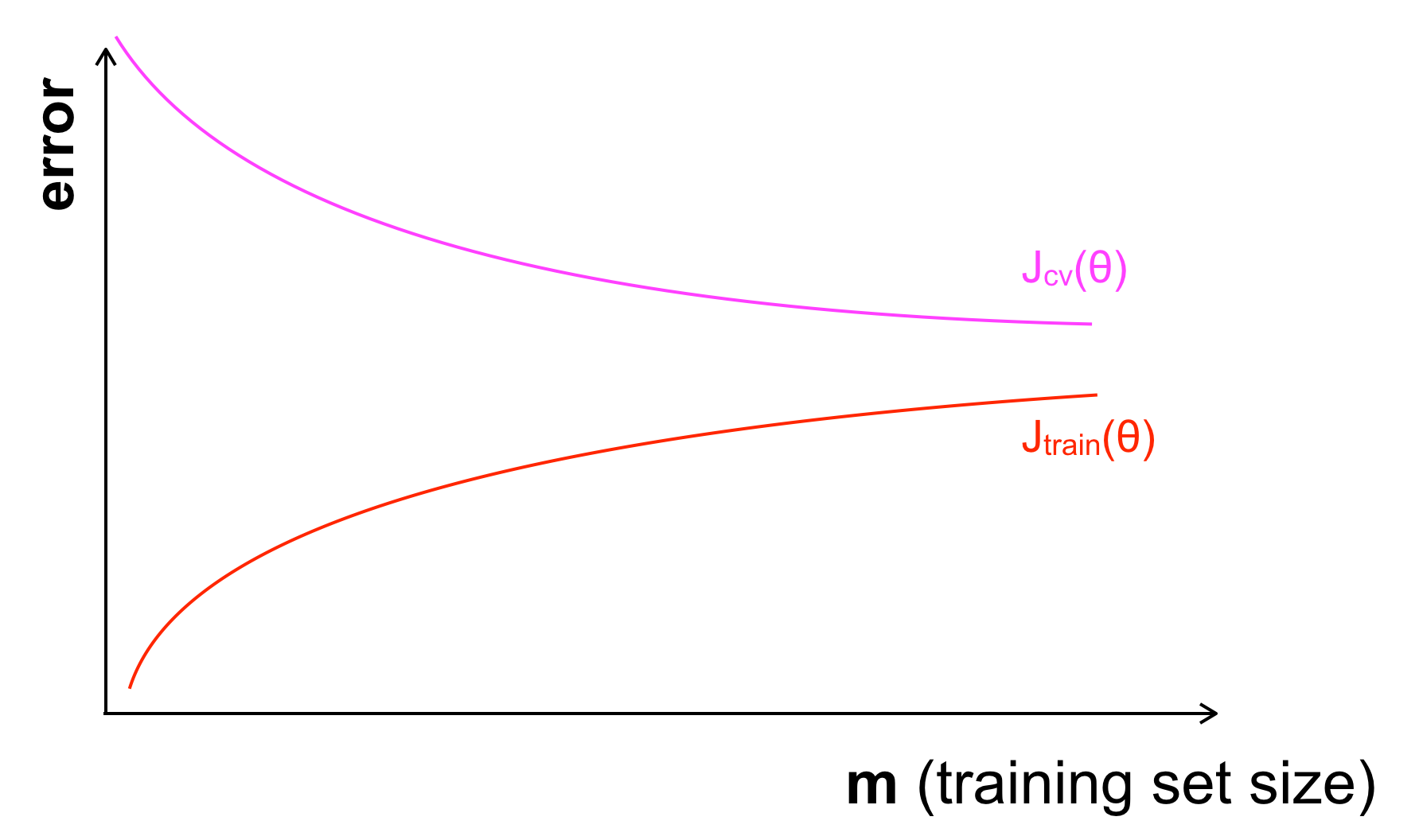
Để ý một chút rằng:
- Với tập training, \(J_{train}\) sẽ nhỏ khi số lượng dữ liệu nhỏ (Với càng ít dữ liệu, mô hình của ta càng dễ dự đoán đúng nhiều trên tập training) và khi \(m \space J_{train}\) cũng tăng theo.
- Với tập CV, \(J_{cv}\) sẽ lớn khi số lượng dữ liệu training nhỏ (Với ít dữ liệu, mô hình của ta sẽ khó tổng quát hoá được để dự đoán xu hướng của dữ liệu nên khi test trên tập CV, sai số sẽ lớn) và ngược lại khi \(m\) tăng, \(J_{cv}\) sẽ giảm.
Hai điều trên có nghĩa sai số trên tập training và CV sẽ càng ngày càng tiến gần tới nhau. Giá trị của 2 giá trị này càng gần nhau, nghĩa là mô hình đang học một cách phù hợp. Ngược lại khi gặp vấn đề Underfitting hay High Bias thì đồ thị sẽ trông giống như sau:
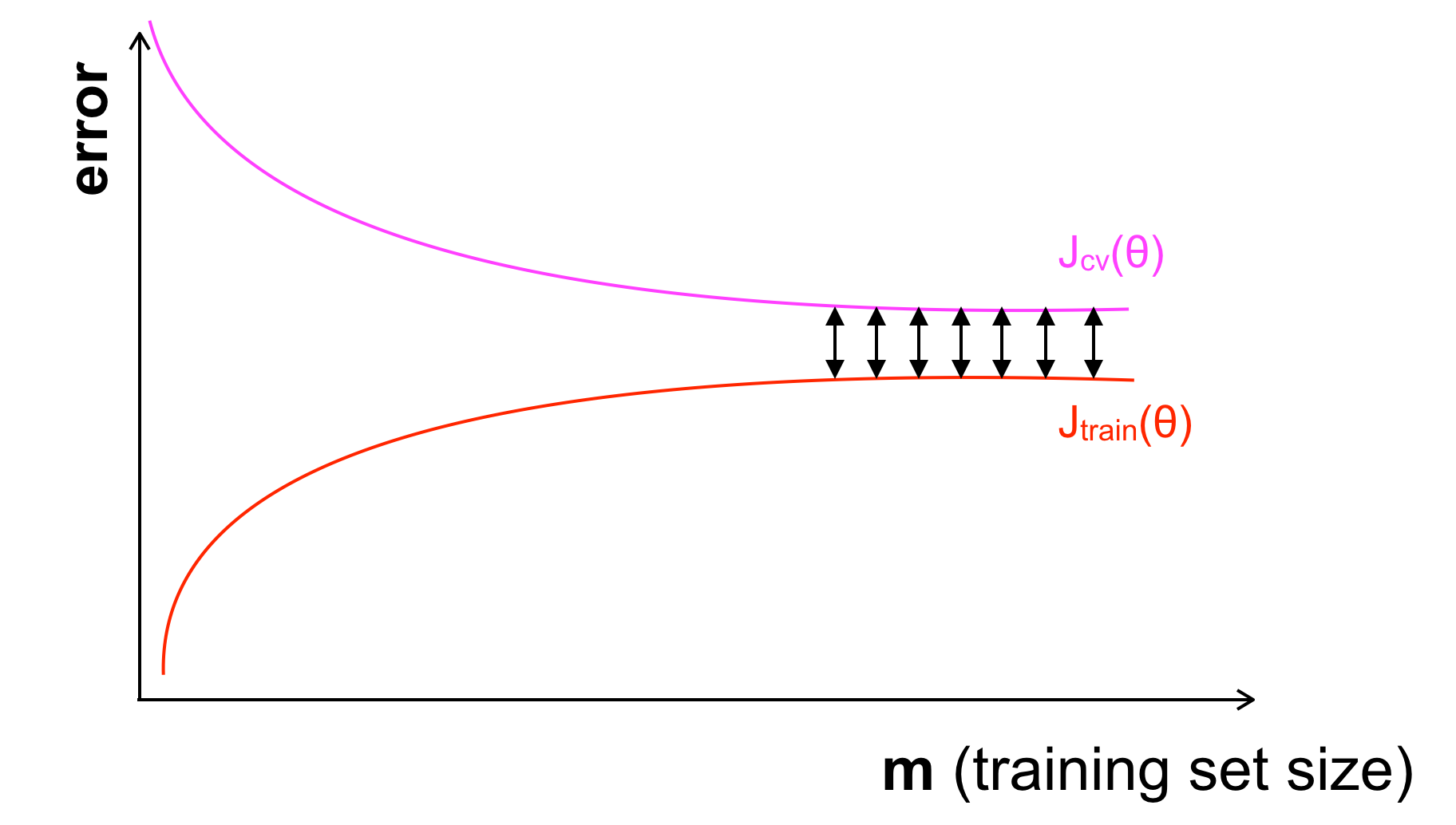
Khi vướng vào Underfitting (High Bias): \(J_{train}\), \(J_{cv}\) đều lớn, mà Underfitting là khi mô hình của ta quá đơn giản hoặc không phù hợp nên khi lượng dữ liệu có tăng lên, sai số trên cả 2 tập cũng không thể giảm. Như trên đồ thị ta thấy, \(J_{train}\) và \(J_{cv}\) đạt ngưỡng và không tiến lại gần nhau nữa. Khi gặp vấn đề Overfitting hay High Variance thì đồ thị lại khác:
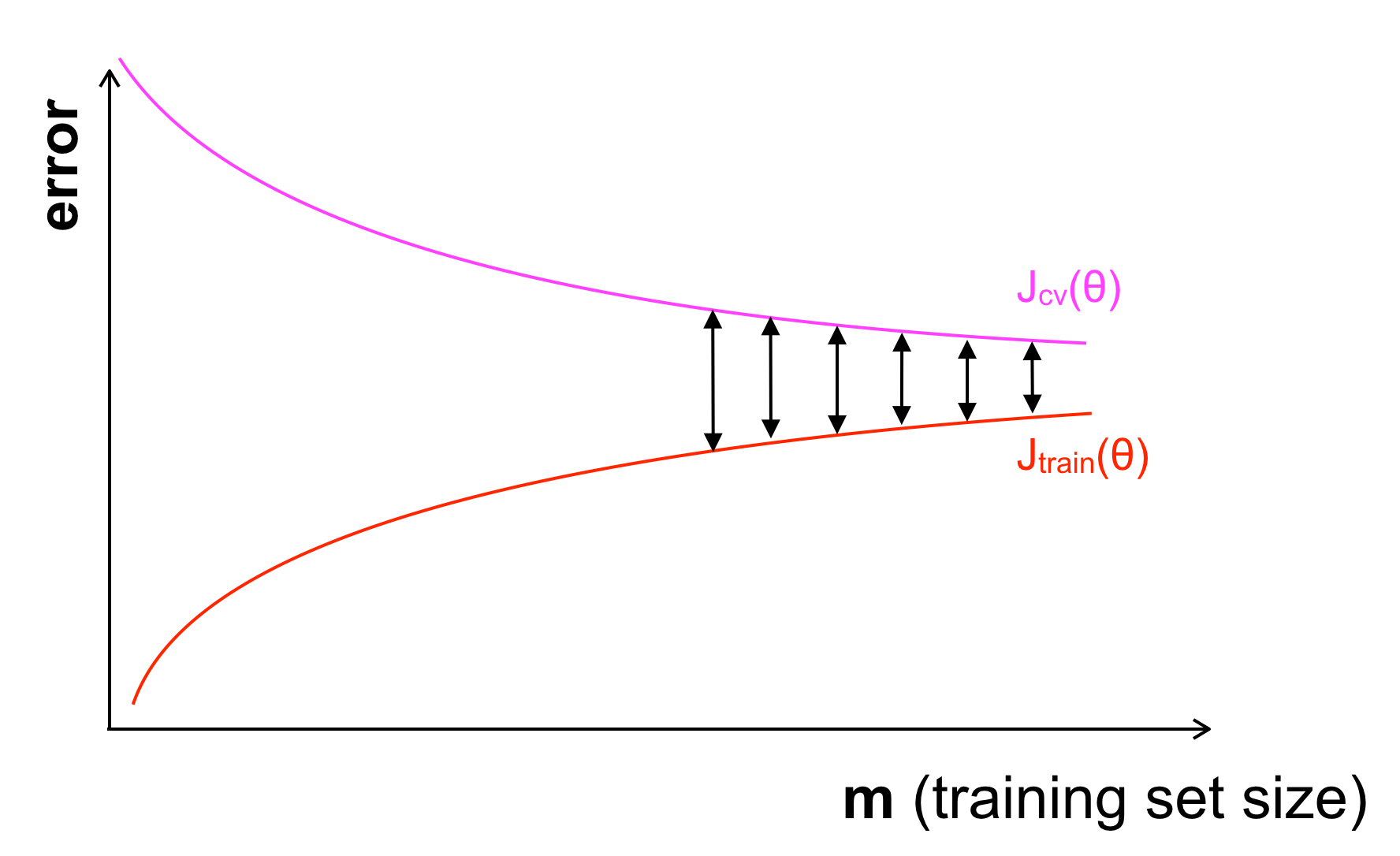
Khi gặp phải Overfitting (High Variance): \(J_{train}\) nhỏ nhưng \(J_{cv}\) lại lớn. Ở thời điểm hiện tại, mô hình của ta học tốt trên tập training, có thể dự đoán tốt trên tập training nhưng trên tập CV vẫn còn chưa tốt, tuy nhiên \(J_{train}\) và \(J_{cv}\) vẫn đang có xu hướng tiến lại gần nhau khi \(m\) tăng. Nghĩa là trong trường hợp này, khi tăng số lượng dữ liệu có lẽ sẽ giải quyết đc vấn đề. (Khi \(m\) đủ lớn, sai số trên 2 tập sẽ gần như bằng nhau). Tuy nhiên, khi tăng số lượng dữ liệu chỉ có thể có tác dụng chứ không chắc chắn vì ngoài ra ta còn gặp các vấn đề khác như \(\lambda\) quá nhỏ, bậc mô hình quá cao…
7. Recap:
Ta sẽ cùng tổng kết một số phương pháp và tác dụng của nó đối với High Bias & High Variance:
- Tăng số lượng dữ liệu: có thể giúp fix High Variance, nhưng không có ý nghĩa gì với High Bias
- Giảm số lượng feature: fix High Variance (như trong bài về Regularization ta đã đề cập)
- Tăng số lượng feature: fix High Bias (tăng số lượng feature giúp mô hình phức tạp hơn)
- Thêm thành phần đa thức: fix High Bias (thực tế là một hình thức tăng số lượng feature, và tăng độ phức tạp của mô hình)
- Giảm \(\lambda\): fix High Bias (tránh việc Regularization triệt tiêu toàn bộ các feature)
- Tăng \(\lambda\): fix Hight Variance (tránh việc bỏ qua Regularization) Đối với ANN:
- Sử dụng NN nhỏ, ít layer, ít neurons – chi phí tính toán rẻ, dễ vướng vào Underfitting do sự đơn giản
- Sử dụng NN lớn, nhiều layer, nhiều neurons – dễ vướng vào Overfitting tuy nhiên có thể giải quyết bằng Regularization, chi phí tính toán lớn
Với những quan sát trên, chúng ta đã phần nào tự tin hơn vào khả năng “chẩn bệnh” cho mô hình của mình. Cảm ơn các bạn đã quan tâm theo dõi và hẹn gặp lại các bạn trong bài viết sau.
