[ML – 15] From Sigmoid function to Rectifier Linear function
Chào các bạn, hôm nay chúng ta tiếp tục loạt bài về ML, từ đầu tới giờ ta đã đề cập tới một số loại hàm activation (là những hàm số ta có thể đưa vào ANN để trở thành một neuron) như hàm tuyến tính (trong Linear Regression), hàm sigmoid (trong Logistic Regression), Step function (để gán nhãn cho output của Logistic Regression). Trong bài viết này tôi muốn đề cập tới một hàm số mới có tên gọi Rectifier (unit hay neron sử dụng hàm này được gọi là ReLU – Rectifier Linear Unit). Hãy cùng tìm hiểu xem hàm số này làm được gì và tại sao người ta lại sử dụng nó.
1. Sigmoid Function:
Ta nhắc lại hàm sigmoid:

Với cost function:
\[\begin{align*} J(\theta) = \Big \{ \begin{array}{l} -log(h(x)) \space & (if \space y = 1) \\ -log(1 - h(x)) \space & (if \space y = 0) \end{array} \end{align*}\]Ta thử vẽ đồ thị cho \(J(\theta)\):
\(J(\theta) = \space – log(h(x)) \space \space \space (if \space y = 1)\)
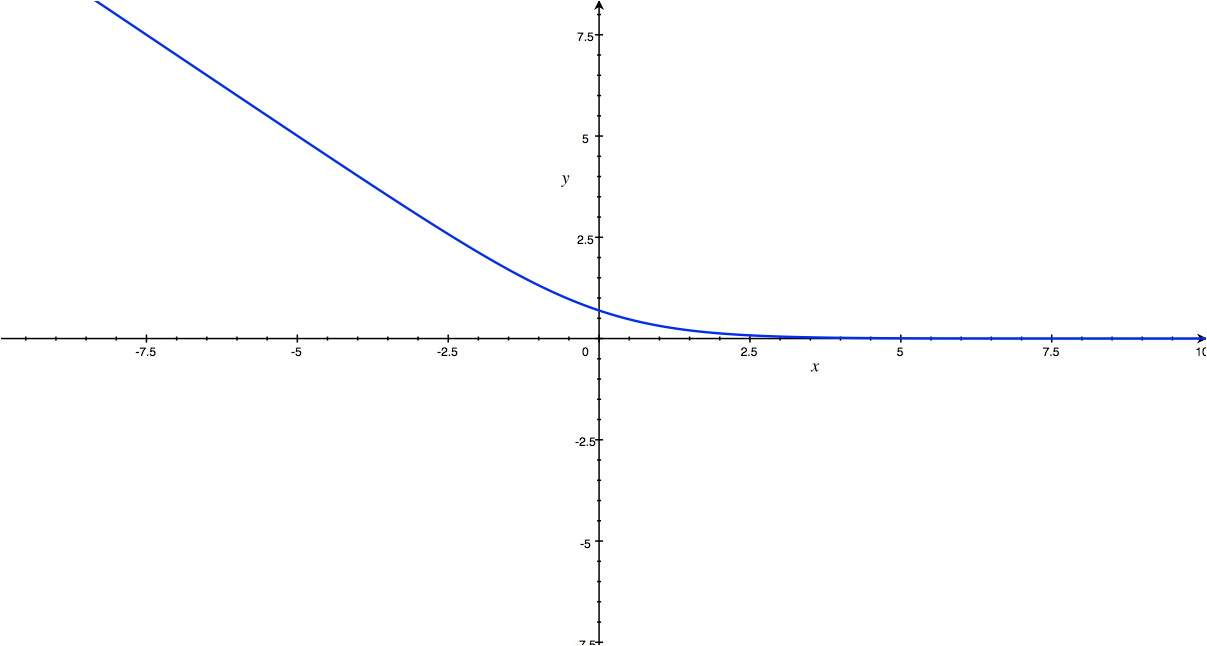
\(J(\theta) = \space – log(1 - h(x)) \space \space \space (if \space y = 0)\)
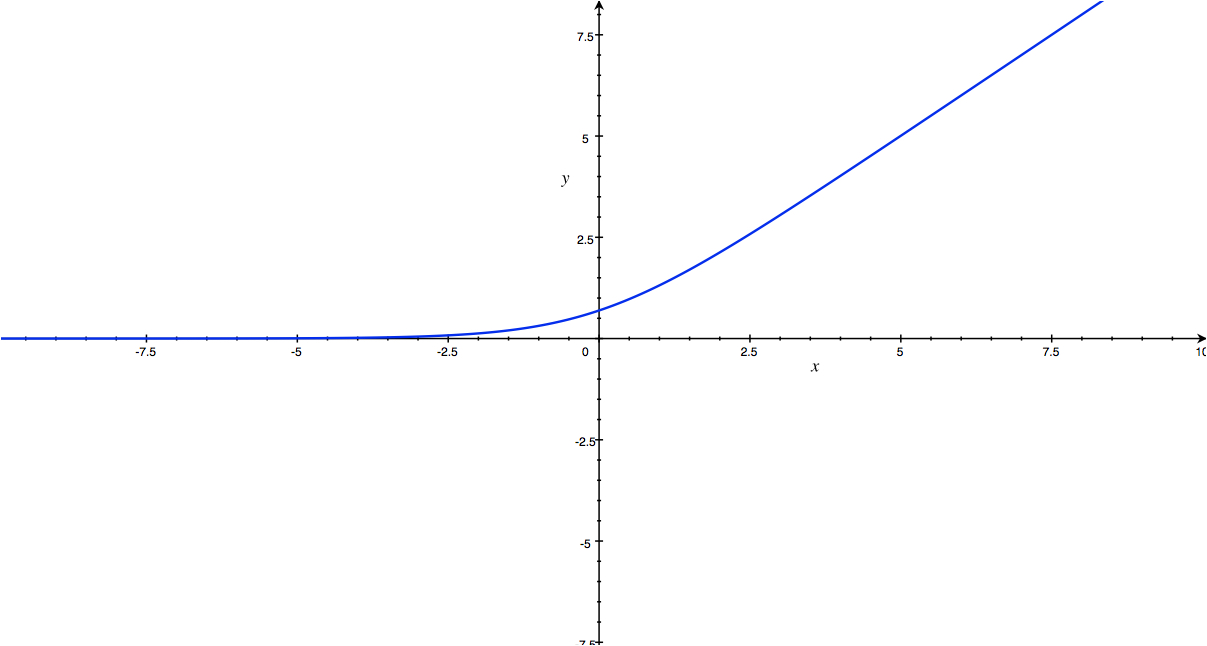
Các bạn sẽ thấy 2 phần riêng biệt của cost function khi \(y = 0\) và \(y = 1\) đối xứng nhau. Hãy thu gọn giá trị trên 2 hàm số này:
\[\begin{align*} y & = -ln (1 - \frac{1}{1 + e^{-x} }) = -ln(\frac{e^{-x}}{1 + e^{-x}}) = -ln(\frac{1}{e^{x} + 1}) = -ln(1) + ln(1 + e^{x}) = 0 + ln(1 + e^{x}) = ln(1 + e^{x}) \\ y & = -ln(\frac{1}{1 + e^{-x}}) = -ln(1) + ln(1 + e^{x}) = 0 + ln(1 + e^{-x}) = ln(1 + e^{-x}) \end{align*}\]Cả 2 trường hợp \(y = 0\) và \(y = 1\), cost function của ta đều là hàm số \(ln(1+e^x)\) nhưng nhận giá trị của x đối xứng nhau (ngược dấu nhau). Vậy hàm số \(ln(1+e^x)\) có gì đặc biệt, điểm đặc biệt là khi \(x\) tiến về \(+∞\) thì giá trị hàm số tiến về \(+∞ \) còn khi \(x\) tiến về \(-∞\) thì hàm số tiến về \(0\). Nó được đặt tên là Softplus. Vậy hàm số này có liên hệ như thế nào với Rectifier Linear function ?
2. Rectifier Linear function:
Hàm số \( f(x) = max(0, x) \) được gọi là Rectifier Linear (ReL) function. Điểm đặc biệt của hàm số này là giá trị của nó xấp xỉ với giá trị của hàm Softplus. Thật vậy: \(ln(1+e^x) ≈ ln(e^x) = x\). Khi \(x\) càng lớn, càng gần tới \(+∞\) thì hàm Softplus có giá trị càng gần với ReL. \(ln(1+e^x) ≈ ln(1) = 0\). Khi \(x\) càng nhỏ, càng gần tới \(-∞\) Ta cùng xem đồ thị của hàm ReL như thế nào:
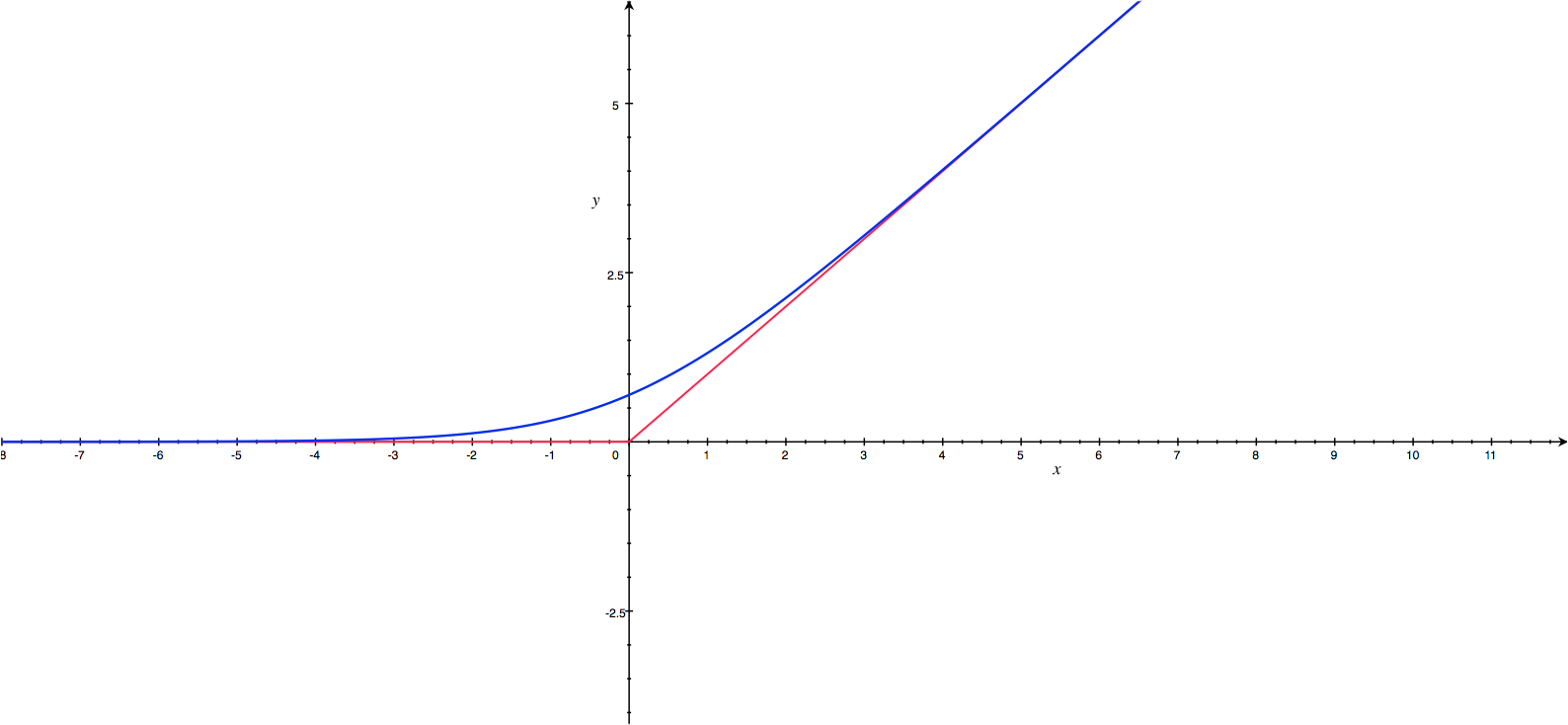
ReL giúp cho giá trị của hàm số tiến tới \(0\) và \(+∞\) nhanh hơn, hay nói cách khác giúp cho giá trị tiên đoán tránh xa khỏi ngưỡng (threshold), sẽ gần với 2 nhãn \(0\) và \(1\) hơn. Hàm số này sẽ giúp phát triển Logistic Regression lên SVM (Support Vector Machine), hay giúp thay thế hàm sigmoid trong nhiều mô hình và đặc biệt giúp khắc phục vấn đề trong quá trình Gradient Descent (tôi sẽ đề cập trong bài viết khác). Hàm ReL còn có một số dị bản khác, các bạn thể tham khảo để sử dụng cho phù hợp.
