[ML – 16] Rectifier Linear function and Vanishing Gradient Problem
Chào các bạn, trong bài viết trước ta đã đề cập tới một hàm activation mới Rectifier Linear, trong mạng Neural nó được kí hiệu là ReLU (Rectifier Linear Unit) đồng thời tôi cũng có nhắc tới việc ReLU giúp giải quyết vấn đề trong Gradient Descent, vậy vấn đề ở đây là gì, và ReLU giải quyết nó như thế nào ? Trong bài viết này chúng ta sẽ thử cùng nhau tìm hiểu chúng.
1. Vanishing Gradient Problem:
Dịch ra có nghĩa là Gradient của hàm số bị bốc hơi, hay nói cách khác đạo hàm quá nhỏ, gần như bằng 0. Vậy vấn đề này xảy ra khi nào ? Nếu trong mạng NN với giải thuật Back Propagation, ta tạm coi như tất cả các hàm activate của các neuron là hàm sigmoid. Để đơn giản, ta sẽ bỏ qua bias, và mỗi layer sẽ chỉ sử dụng 1 unit (1 neuron).
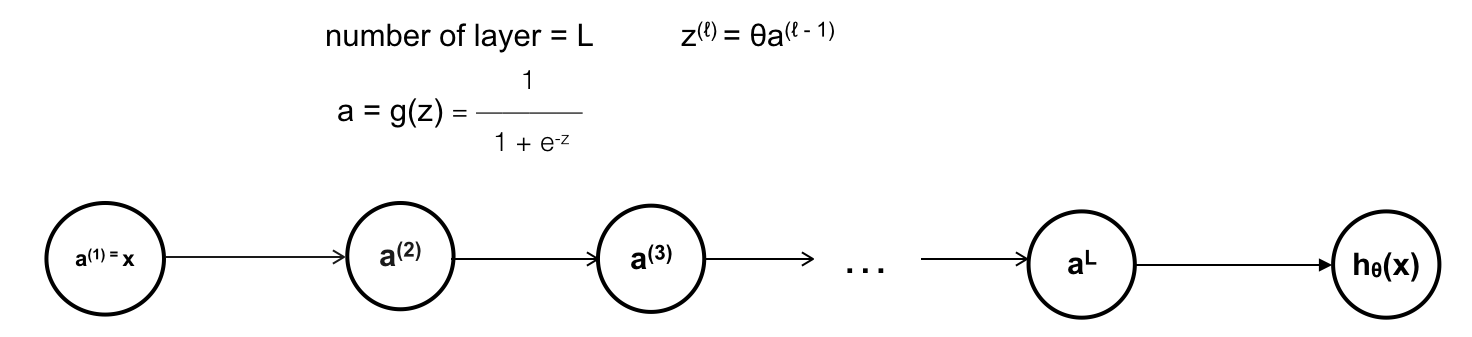
Giờ ta tính thử xem đạo hàm tại các neurons, hay đạo hàm trên các trọng số \(\theta^{ℓ}\):
\[ \frac{dJ}{d \theta ^{(ℓ)}} = \frac{dJ}{da^{(L)}} . \frac{da^{(L)}}{dz^{(L)}} . \frac{dz^{(L)}}{da^{(L-1)}} . \frac{da^{(L-1)}}{dz^{(L-1)}} … \frac{da^{(ℓ + 1)}}{dz^{(ℓ + 1)}} . \frac{dz^{(ℓ + 1)}}{d \theta ^{(ℓ)}} \]
Ta hãy để ý, với phần đạo hàm của a với biến z (chính là đạo hàm của hàm sigmoid) xuất hiện nhiều lần trong việc tính Back-propagation, số lượng layer của mạng NN càng nhiều thì số lượng đạo hàm của hàm sigmoid được sử dụng trong việc tính đạo hàm trên các trọng số càng nhiều, các trọng số càng gần lớp input sẽ phải nhân thêm với nhiều đạo hàm của hàm sigmoid.
\[ \frac{da^{(ℓ)}}{dz^{(ℓ)}} = \frac{dg’(z^{(ℓ)})}{dz^{(ℓ)}} = g(z^{(ℓ)}).(1 - g(z^{(ℓ)})) \]
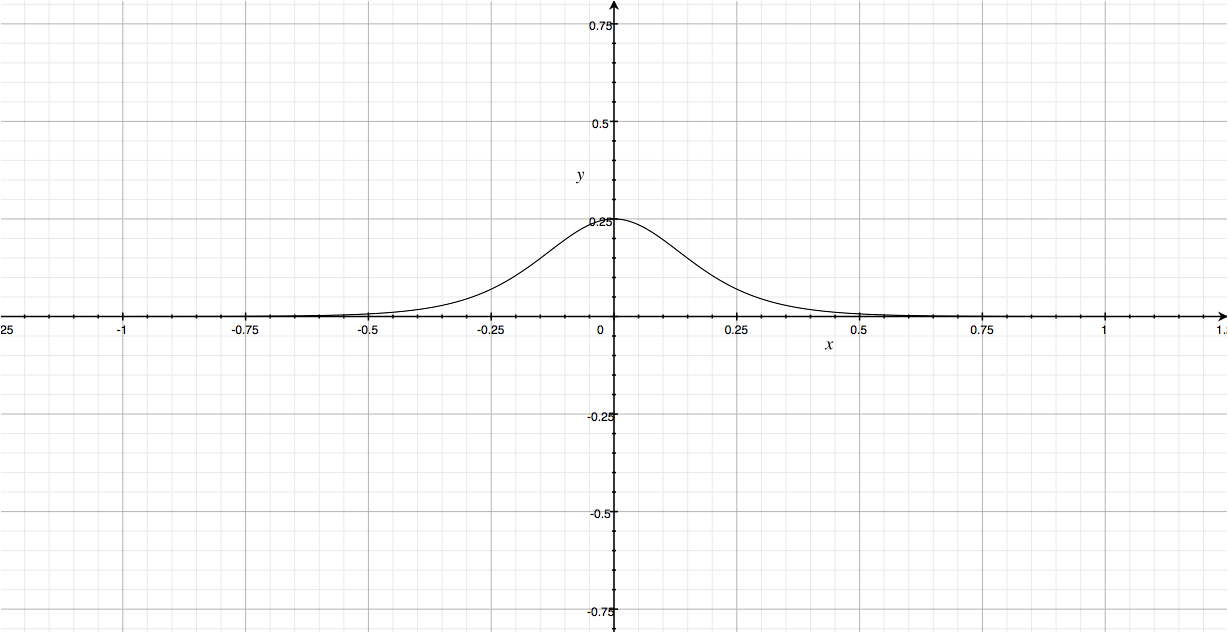
Đồ thị bên trên chính là đồ thị đạo hàm của hàm sigmoid. Các bạn dễ dàng thấy rằng giá trị của hàm số này chỉ nằm trong khoảng [0,0.25]. Điều này có nghĩa rằng cứ mỗi khi đi qua một layer có chứa hàm sigmoid, đạo hàm của các trọng số sẽ nhận giá trị tối đa chỉ = \(\frac{1}{4}\) so với trước đó. Nghĩa là càng gần lớp input, giá trị đạo hàm càng nhỏ, nếu mạng NN có chứa nhiều lớp với các unit là sử dụng hàm sigmoid làm hàm activation, các trọng số của các unit này sẽ gần như không được update, hay update quá chậm, số lượng vòng lặp ta cần để training càng nhiều, thậm chí bất khả thi. Vậy ta nên xử lý vấn đề này như thế nào ?
2. Solution with ReLU:
Giải pháp tốt nhất hiện tại chính là sử dụng hàm ReLU thay thế cho hàm Sigmoid. Tại sao vậy, ta thử tính đạo hàm cho ReLU:
\[f(x) = \Big \{ \begin{array}{l} x \space \space \space (if \space x > 0)\\ 0 \space \space \space (if \space x < 0) \end{array} \\ \\ \\ f'(x) = \Big \{ \begin{array}{l} 1 \space \space \space (if \space x > 0)\\ 0 \space \space \space (if \space x < 0) \end{array}\]Vậy là chỉ trừ khi \(x < 0\), còn lại đạo hàm của hàm ReLU đều \(= 1\), vấn đề được giải quyết. Tuy nhiên với \(x < 0\), thì tuyệt nhiên các trọng số không được update nữa. Để giải quyết vấn đề này, ta có thể sử dụng các biến thể của ReLU như Leak ReLU (thay vì \(= 0 \) khi \(x < 0\) thì \(f(x) = 0.01x\) khi \(x < 0\) – con số \(0.01\) có thể thay đổi để sử dụng cho phù hợp)
