[ML – 17] Neural Net Regularization with Drop-Out
Chào các bạn, rất vui được gặp lại các bạn trong bài viết này. Hôm nay chúng ta sẽ tìm hiểu về một kĩ thuật Regularization cho ANN được gọi là Drop-Out. Thay vì đi vào tìm hiểu “đạo lý” đằng sau kĩ thuật này hay phân phối xác suất đằng sau nó, tôi sẽ giải thích một cách trực quan để các bạn dễ hiểu, dễ nắm bắt và mường tượng được ý nghĩa của nó.
1. Drop-Out là gì:
Như ta đã biết overfitting là một vấn nạn đối với Machine Learning, đặc biệt là trong mạng NN. Khi muốn cho mô hình trở nên phức tạp hơn, ta thường tăng số lượng layer và số lượng unit của mỗi layer thay vì tăng bậc của feature như trước đây đã đề cập. Nhưng khi mô hình phức tạp hơn, overfitting bắt đầu xuất hiện, vì số lượng tham số trong mạng NN nhiều và có “độ sâu” khác nhau, vì vậy khi áp dụng chung 𝝺 cho tất cả các tham số sẽ yêu cầu số lần training lớn để tìm được 𝝺 phù hợp. Có một kĩ thuật dành riêng cho mạng NN và khá đơn giản, đó là Drop-out (một kĩ thuật khác được biết đến tương tự là Drop-Connect). Drop-out là một kĩ thuật Regularization để chống lại vấn đề overfitting. Cách Drop-out thực hiện là xoá bỏ một số unit trong các step training ứng với một giá trị xác suất p cho trước.
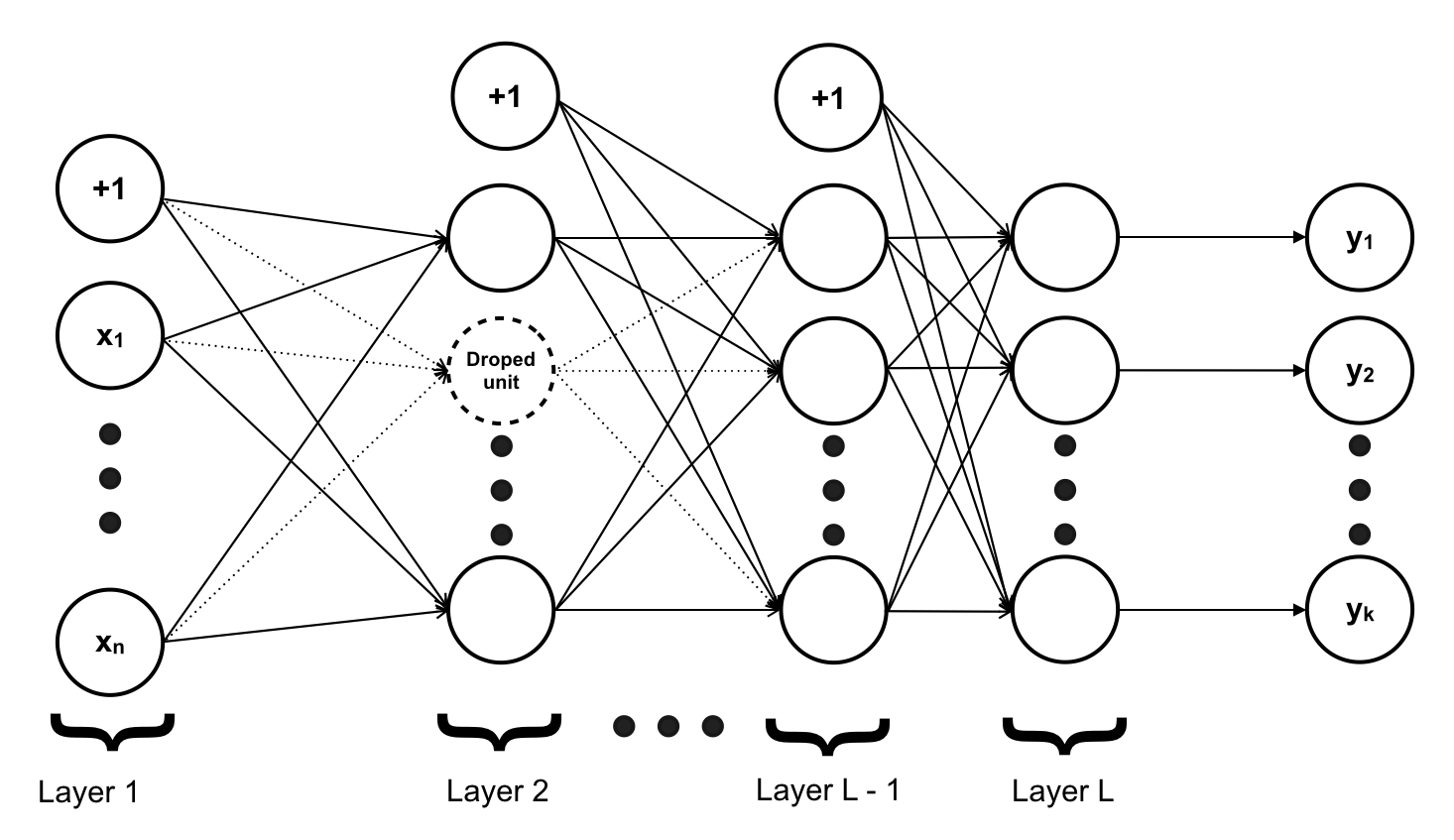
2. Drop-Out hoạt động như thế nào:
Drop-Out được áp dụng trên một layer của mạng NN với một xác suất p cho trước (ta có thể sử dụng nhiều Drop-Out khác nhau cho những layer khác nhau, nhưng trên 1 layer sẽ chỉ có 1 Drop-Out). Tại mỗi step trong quá trình training, khi thực hiện Forward Propagation (Lan truyền xuôi) đến layer sử dụng Drop-Out, thay vì tính toán tất cả unit có trên layer, tại mỗi unit ta “gieo xúc xắc” xem unit đó có được tính hay không dựa trên xác suất p. Với những unit được tính, ta tính toán bình thường còn với những unit không được tính giá trị tại unit đó = 0. Khi thực hiện tính toán trên mạng NN trong quá trình test (sử dụng mạng NN để dự đoán) thay vì làm như trên, ta thực hiện tính toán trên tất cả các unit nhưng trọng số trên mỗi connect đến các unit của layer được áp dụng Drop-Out được thay thế bằng giá trị của trọng số đó với xác suất p hay \(θ := θ * p\)
3. Tại sao Drop-Out hiệu quả:
Đối với mạng NN, không giống như những kĩ thuật khác như Linear Regression hay Logistic Regression là đẩy bậc của feature lên mà ta tăng số lượng hidden layer và số lượng unit trong các layer lên. Nhưng đối khi do việc thêm vào quá nhiều hidden layer cũng như unit khiến cho mô hình phức tạp hơn mức cần thiết và khiến chúng bị overfitting. Chính vì vậy để tránh bị overfitting trong trường hợp này, ta cần phải giản lược mạng NN hiện có. Khi áp dụng Drop-Out vào 1 layer nào đó, thì thực tế tại mỗi training step mạng NN của ta chỉ còn 1 phần:
Giả sử layer của ta có 4 unit (như trong clip minh hoạ), và xác suất p = 0.8 -> khi đó xác suất sử dụng số lượng unit của layer sẽ như sau:
- Sử dụng 0 unit của layer:
\(= 1 * (1-p)^4 * p^0 = 0.2^4 * 0.8^0 = 0.0016 \)
(Vì xác suất để mỗi unit không được sử dụng là \(1-p\) nên để cả 4 unit không được sử dụng thì xác suất phải là \((1-p)^4\) và chỉ có \(C_4^0\) = 1 khả năng chọn ra 0 unit được sử dụng) - Sử dụng 1 unit của layer:
\(= 4 * p^1 * (1-p)^3 = 4 * 0.8^1 * 0.2^3 = 0.0256 \)
(Vì xác suất để mỗi unit không được sử dụng là \(1-p\) nên để 3 unit không được sử dụng thì xác suất phải là \((1-p)^3\) và có thêm 1 unit được sử dụng với xác suất \(p\), bên cạnh đó có tới \(C _{4} ^{1} = 4\) unit có thể được chọn để sử dụng) - Tương tự khi sử dụng 2 unit của layer:
\(= 6 * p^2 * (1-p)^2 = 6 * 0.8^2 * 0.2^2 = 0.1536\)
(có \(C_4^2 = 6\) cách để lựa chọn 2 unit để sử dụng trong 4 unit của layer) - Khi sử dụng 3 unit của layer:
\(= 4 * p^3 * (1-p)^1 = 4 * 0.8^3 * 0.2^1 = 0.4096 \)
(có \(C_4^3 = 4\) cách để lựa chọn 3 unit để sử dụng trong 4 unit của layer) - Khi sử dụng 4 unit của layer:
\(= p^4 * (1-p)^0= 0.8^4 * 0.2^0 = 0.4096\)
(chỉ có \(C_4^4 = 1\) cách để lựa chọn 4 unit để sử dụng trong 4 unit của layer)
Tại mỗi training step, ta sử dụng mạng với lượng neuron khác nhau, chính vì vậy model của ta không thể hoàn toàn “tin tưởng” vào một neuron nào hay feature cụ thể nào của layer đó. Đây cũng là một lý do để mô hình giảm thiểu việc bị overfit. Bên cạnh đó, với xác suất p ta cũng có được lượng neuron trung bình cần sử dụng tại layer này:
\[E(number \space of \space unit) = 0 * 0.0016 + 1 * 0.0256 + 2 * 0.1536 + 3 * 0.4096 + 4 * 0.4096 = 3.2 = 4 * 0.8 = 4 * p\]
(Số lượng unit nhân với xác suất \(p\)). Nghĩa là khi áp dụng Drop-Out layer của ta chỉ sử dụng số unit tương đương \(3.2\) bằng cách sử dụng nhiều mạng nhỏ (với 0,1,2,3,4 unit trong layer như mô tả ở trên) Có 2 điểm lợi khi ta sử dụng Drop-Out:
- Với việc sử dụng xác suất p, lượng unit bạn mong muốn sử dụng có thể tùy ý, không nhất thiết phải là số tự nhiên. Trong khi với việc thay đổi trực tiếp số lượng neuron, bạn chỉ có thể có số lượng neuron là số tự nhiên.
- Dù tương đương với việc sử dụng 3.2 unit như ở trên, nhưng trong quá trình training ta lại sử dụng xác suất p để giữ lại các neuron nên, model không thực sự sử dụng cụ thể một lượng unit nhất định. Khi số step training lớn, thực tế ta sử dụng model với kết quả là trung bình của các mạng con có số lượng neuron từ 0 - 4 và với trọng số là xác suất như đã mô tả ở trên. Điều này cũng không thể có được khi bạn giảm trực tiếp lượng unit của layer.
Cuối cùng, các bạn sẽ thắc mắc tại sao khi sử dụng mạng NN để test ta lại không “gieo xúc xắc” như khi training mà lại sử dụng trọng số có giá trị bị scale theo xác suất p.
Nếu muốn thực hiện tương tự như quá trình training, bạn sẽ phải thực hiện predict “nhiều” lần, và lấy giá trị trung bình của tất cả các lần predict đó. Điều này khiến cho hệ thống của ta chậm đi nhiều lần, chưa kể để có nhiều kết quả đủ để thể hiện xác suất p, số lần thực hiện sẽ rất lớn. Vậy bây giờ phải làm như thế nào để chỉ phải predict 1 lần, nhưng cho kết quả gần đúng nhất. Giả sử như ta thực hiện predict nhiều lần, và có 4 unit A,B,C,D tương ứng trọng số W của chúng là \(W_a, W_b, W_c, W_d\). Giờ hãy xem với 1 trọng số cụ thể là Wa, nó được sử dụng như thế nào!
- Xác suất unit A được sử dụng trong trường hợp cả layer giữ lại cả 4 unit là 100%. Xác suất giữ lại 4 unit = 0.4096
- Xác suất unit A được sử dụng trong trường hợp chỉ có 3 unit được giữ lại là 75%. Xác suất giữ lại 3 unit = 0.4096
- Xác suất unit A được sử dụng trong trường hợp chỉ có 2 unit được giữ lại là 50%. Xác suất giữ lại 2 unit = 0.1536
- Xác suất unit A được sử dụng trong trường hợp chỉ có 1 unit được giữ lại là 25%. Xác suất giữ lại 1 unit = 0.0256
=> \( W_a ^T A \) trước kia sẽ trở thành: \( = 0.4096 * 1 * W_a ^T A + 0.4096 * 0.75 * W_a ^T A + 0.1536 * 0.5 * W_a ^T A + 0.0256 * 0.25 * W_a ^T A \)
\( = 0.8 * W_a ^T A \)
=> Ta phải scale W theo 0.8 = p
Đến đây chúng ta đã hiểu tường tận Drop-Out rồi phải không nào :)
