[ML – 19] Convolution Neural Network – Part 2
Chào các bạn, hôm nay chúng ta tiếp tục tìm hiểu về mạng neural tích chập (CNN). Trong bài viết trước, ta đã được biết về những nhược điểm trong mạng neural truyền thống đồng thời giới thiệu về CNN và đã có được những cái nhìn đầu tiên về mô hình Deep Learning này. Hôm nay chúng ta sẽ tìm hiểu cách CNN hoạt động. Nếu như sau bài viết trước các bạn có đi tìm hiểu về “convolution” (tích chập) là gì thì với những ai đã “quên” hầu hết toán sẽ cảm thấy vô cùng tuyệt vọng, bản thân tôi cũng cảm thấy như vậy trong lần đầu mở nội dung về convolution trên wiki ra đọc. Tuy nhiên nếu đã tìm hiểu, bạn sẽ thấy để hiểu tích chập, ta phải biết tích phân là gì đã 🙂
1. Integral (Tích phân):
Như trong những bài viết đầu tiên, ta đã hiểu thế nào là slope hay gradient của một đoạn thẳng, từ đó phát triển lên đạo hàm của hàm số tại một điểm. Vậy là từ một hàm số f(x) cho trước ta có thể quan sát được xu hướng tăng hay giảm của nó thông qua việc tăng hay giảm x. Bây giờ câu hỏi đặt ra là nếu ta có đạo hàm của hàm số f(x) tại x liệu ta có thể quan sát được f(x) hay không ? Nói một cách khác là khi ta biết độ dốc của f(x) tại các điểm, liệu ta có thể tìm được giá trị của f(x) hay cả hàm số f(x) không ?
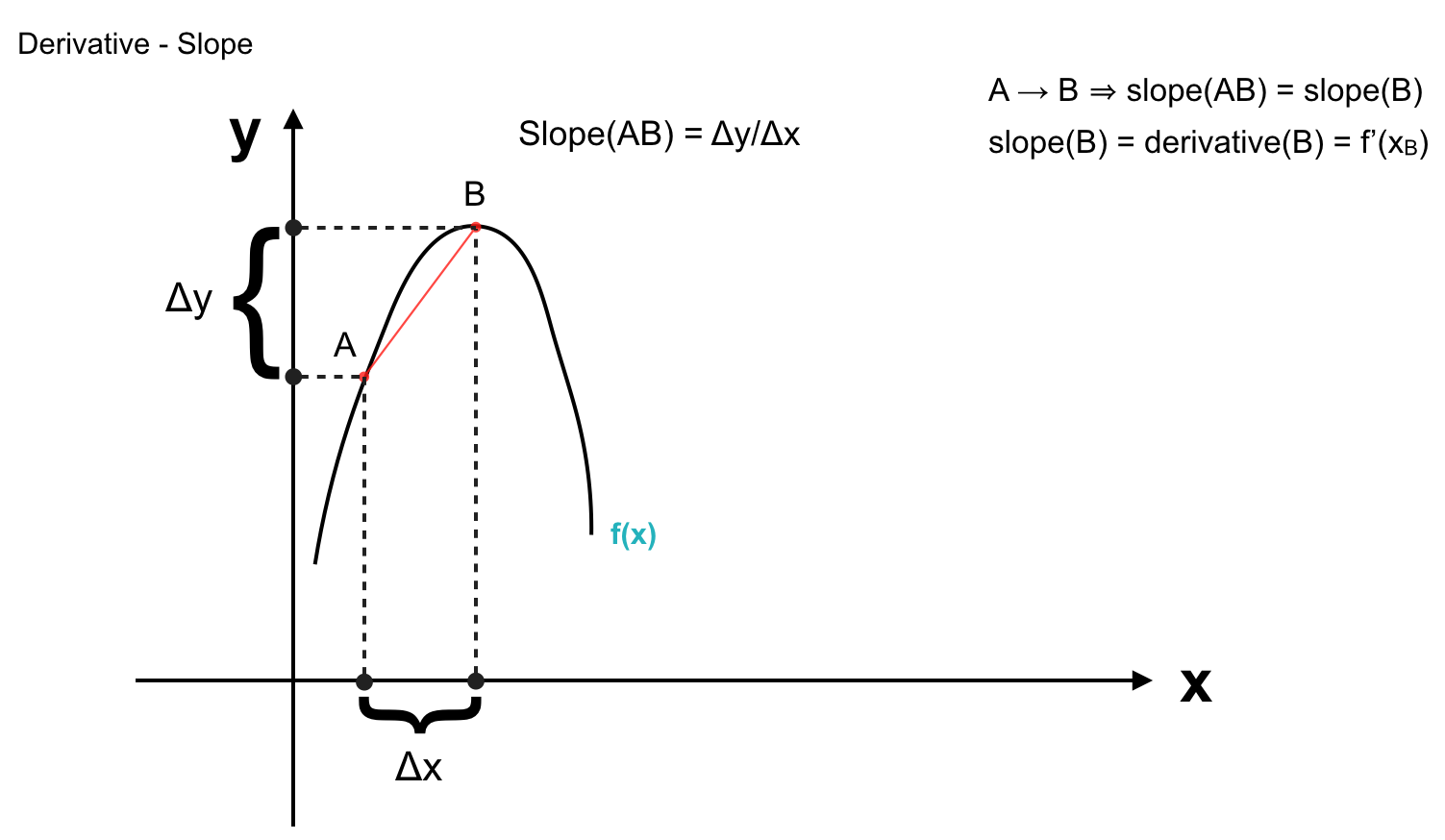
Chú ý rằng, đạo hàm tại một điểm chính là tỉ số giữa thay đổi vô cùng nhỏ trên trục y và thay đổi vô cùng nhỏ trên trục x. Như ở hàm số trên, ta có thể dễ dàng hình dung nó là một hàm bậc 2 nên đạo hàm sẽ là hàm bậc 1 hay tuyến tính – một đường thẳng:
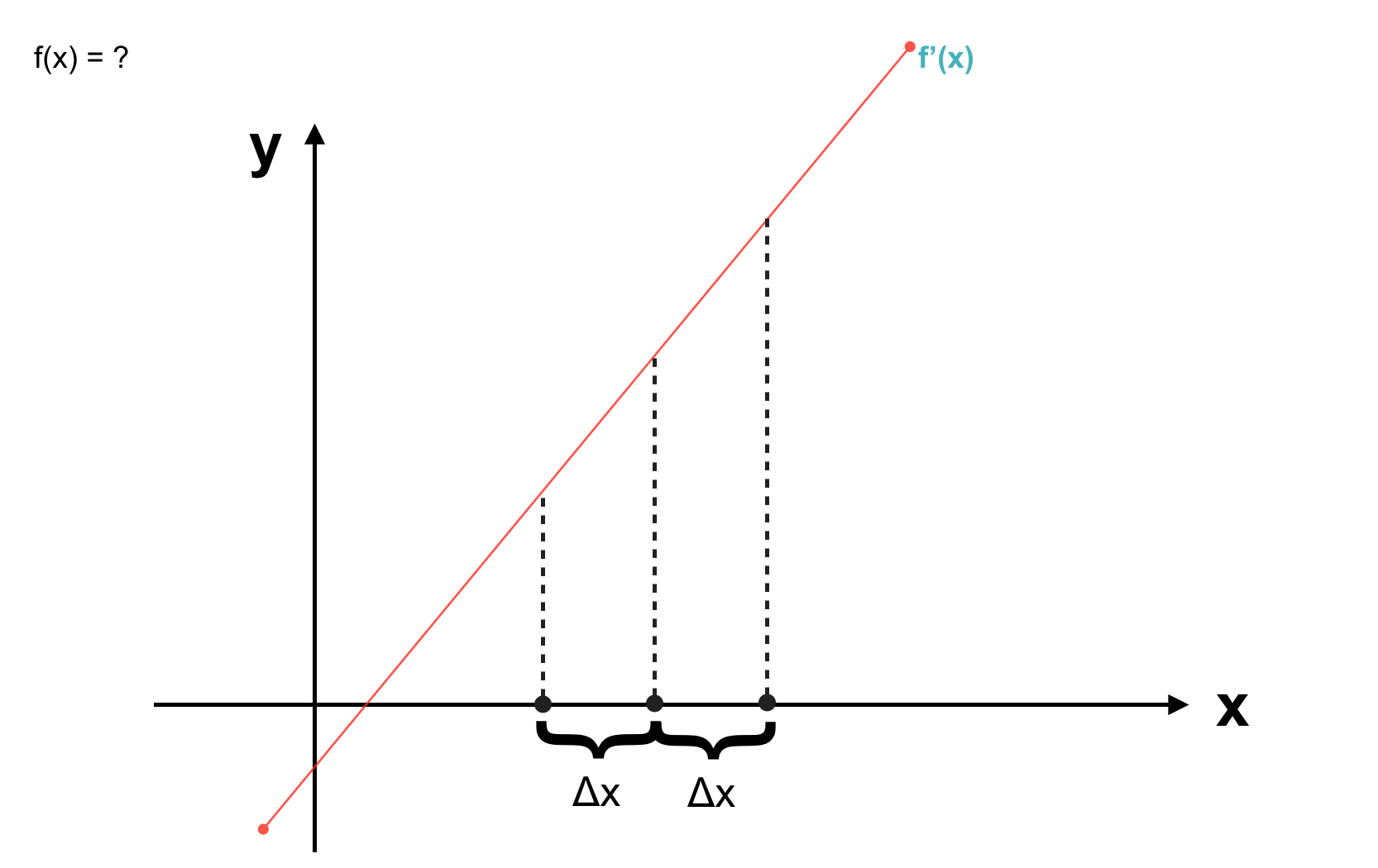
Nếu giả sử rằng (∆x ≈ 0), khi đó nó là khoảng cách giữa 2 điểm liên tiếp trên đồ thị. Ta có đạo hàm tất cả các điểm trên đồ thị của của hàm số f(x) như sau: (Ta bắt đầu từ \(x=a\) và kết thúc ở \(x=b\))
\[\begin{align*} f'(a) & = \frac{[f(a + ∆x) \space – \space f(a)]}{∆x} \\ f'(a + ∆x) & = \frac{[f(a + 2∆x) \space – \space f(a + ∆x)]}{∆x} \\ f'(a + 2∆x) & = \frac{[f(a + 3∆x) \space – \space f(a + 2∆x)]}{∆x} \\ f'(a + 3∆x) & = \frac{[f(a + 4∆x) \space – \space f(a + 3∆x)]}{∆x} \\ & …. \\ f'(a + (b-a)/∆x * ∆x) & = \frac{[f(a + (\frac{b-a}{∆x} + 1)∆x) \space – \space f(a + \frac{b-a}{∆x}∆x)]}{∆x} \end{align*}\]Để ý rằng nếu ta cộng lần lượt tương ứng vế trái với vế trái và vế phải với vế phải ta sẽ có:
\[\begin{align*} \sum _{i=1} ^{m} f'(x + i \Delta x) & = \frac{f(a + (\frac{b-a}{\Delta x} + 1) \Delta x) - f(a)}{\Delta x} \\ & = \frac{f(b+ \Delta x) - f(a)}{\Delta x} \\ & \approx \frac{f(b) - f(a)}{\Delta x} \\ => \sum _{i=1} ^{m} f'(x + i \Delta x) \Delta x & = f(b) - f(a) \end{align*}\]Kết quả cuối cùng, vế trái ở biểu thức trên rất quen thuộc, nó chính là tích phân mà chúng ta phải vật lộn trong những năm tháng thi đại học đó. Dấu \(∫\) trong tích phân chính là đại diện cho dấu \(\sum\) khi số lượng số hạng trong tổng là vô hạn ứng với trường hợp hàm số liên tục. Còn \(∆x\) chính là đại diện cho \(dx\) (viết tắt cho differential x – vi phân trên x hay thay đổi vô cùng nhỏ trên trục x). Thay 2 kí hiệu ta vừa nhắc tới vào, ta được công thức của tích phân 🙂
\[=> \int _{a} ^{b} f'(x)dx = f(b) - f(a) = f(x) \Big | _{a}^{b}\]Vậy tích phân, chính là tổng đạo hàm của tất cả các điểm nằm trên khoảng chúng ta có đạo hàm. Nếu như ta có giá trị của một điểm bắt đầu \(f(a)\), ta có thể tìm được giá trị \(f(b)\) bất kì chỉ với đạo hàm biết trước.
2. Integral in statistic:
Trong thống kê, khi phải làm việc với các giá trị liên tục ta cũng sử dụng tích phân thay thế cho tổng thông thường. Chẳng hạn khi các giá trị là gián đoạn như: Tung xúc xắc 100 lần ta được 20 lần 1, 22 lần 2, 15 lần 3, 16 lần 4, 12 lần 5, 15 lần 6. Vậy trung bình ta sẽ tung xúc sắc được:
\((20 * 1 + 22 * 2 + 15 * 3 + 16 * 4 + 12 * 5 + 15 * 6) / 100 = 323/100 = 3.23\)
Ta viết gọn lại: \(\sum x_k * p_k = 3.23\)
Trong đó: \(x_k\) là các giá trị trên mặt xúc sắc {1,2,3,4,5,6}, còn \(p_k\) là xác xuất rơi vào các mặt được tính trên số lần rơi vào các mặt trên tổng số lần rơi (chẳng hạn mặt 1 có 20 lần rơi thì xác suất = 20/100 = 0.2).
Khi giá trị của \(x\) không còn là các giá trị gián đoạn như trên mặt xúc sắc, giá trị trung bình của các \(x\) (hay mean của x hay E(x)) là tích phân:
\(\int xf(x)d(x)\) trong đó \(f(x)\) là hàm mật độ xác suất (\(p(x) = f(x) * dx\) trong đó \(dx\) rất nhỏ còn \(f(x)\) mô tả xác suất của một \(x\) bất kì trong khoảng \(dx\)).
3. What is convolution:
Tới đây các bạn đã có khái niệm về tích phân. Ta đã có thể hiểu convolution là gì và ý nghĩa của nó trong ML như thế nào. Trên wiki tích chập của 2 hàm số được định nghĩa như sau:
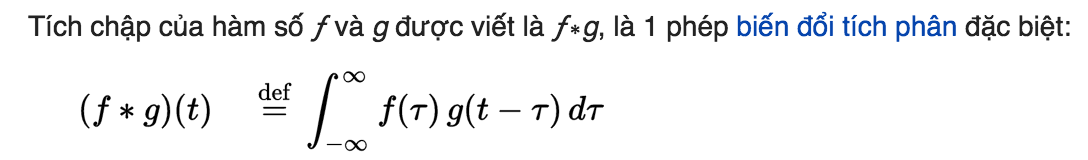
Nhìn vào công thức trên các bạn sẽ khá … “hoang mang”. Tôi sẽ giải thích từng thành phần trong công thức trên: \(𝜏\) : chính là biến \(x\), biến số mà ta sẽ quan sát sự thay đổi hàm số khi \(𝜏\) thay đổi vô cùng nhỏ d𝜏. \(t\) : đây là một biến số khác, trong đó \(f(𝜏)\) đứng im còn \(g(t-𝜏)\) dịch một khoảng \(t\) và bị lật ngược lại, đối xứng qua trục \(y\). Nghĩa là với mỗi \(t\) ta sẽ có một hàm \(g(t-𝜏)\) khác nhau có vị trị đối xứng và lệch đi \(t\) so với hàm \(g(𝜏)\) ban đầu. \(f(𝜏) * g(t-𝜏)\) : tại mỗi t, ta tính tổng của tất cả f và g tại từng \(𝜏\). Vẫn hơi đau đầu phải không ? Giờ nếu bạn nhìn lên phần tích phân trong thống kê bên trên, bạn sẽ thấy tích chập nhìn rất giống \(\int x \space f(x)d(x)\) trong đó \(f(𝜏)\) mô tả \(x\) còn \(g(t-𝜏)\) mô tả xác suất của \(x\). Vậy có nghĩa là nếu đứng từ mặt thống kê tích chập chẳng qua Mean hay Expectation của biến ngẫu nhiên với hàm phân phối xác suất đã biết.
4. Intuition of convolution:
Để các bạn dễ hiểu hơn, tôi sẽ giải thích trên một ví dụ: Giả sử ta có hàm số \(\mathbf{f(x)}\) mô tả vị trí của một người dựa trên thiết bị GPS người đó mang theo (Để cho đơn giản, ta sẽ chỉ thu thập kinh độ của người đó). Tuy nhiên trên thực tế, các thiết bị GPS hoạt động không chính xác 100%, đôi khi có nhiễu, nghĩa là dù ta đứng yên, toạ độ của ta vẫn có thể thay đổi. Chính vì vậy thay vì tạo ra một thiết bị chính xác hơn, ta có thế ước tính vị trị hiện tại thông qua tất cả các vị trí. Cũng giống như trên, tại mỗi \(\mathbf{f(x)}\) ta tạo ra một \(\mathbf{w(t-x)}\) (\(w\) đại diện cho weight) để chỉ trọng số của vị trí đó (tại mỗi thời điểm \(t\), hàm trọng số của ta sẽ khác nhau), \(\mathbf{w(t-x)}\) cao tức xác suất tại thời điểm \(t\) vị trí \(x\) có độ chính xác cao, độ tin cậy cao. Khi tính giá trị trung bình của tất cả các \(\mathbf{f(x) \space w(t-x)} \) ta được vị trị cần ước lượng. Nhưng khi \(x\) là liên tục thì ta cần sử dụng đến tích phân. Hay để ước lượng ta sử dụng tích chập. Vì hàm trọng số \(w\) cũng có giá trị cao tại những \(f(x)\) đáng tin cậy nên \(w\) sẽ phải tương quan với với các vị trí chính xác (\(w\) và xác suất vị trí \(x\) là chính xác phải cùng lớn hoặc cùng nhỏ). Ta có thể hiểu ý tưởng của convolution là sử dụng một hàm trọng số để đánh dấu các giá trị quan trọng (giá trị ước lượng bên trên), hoặc để tìm kiếm các vị trí tương quan của 2 hàm số (các \(t\) mà 2 hàm số tương đương nhau). Như các bạn thấy trên wiki:
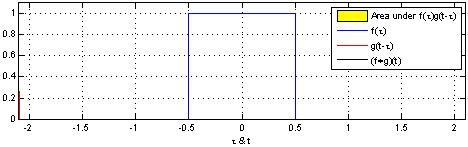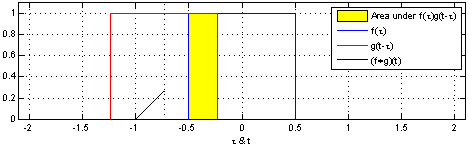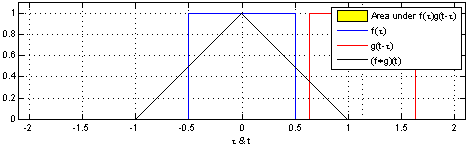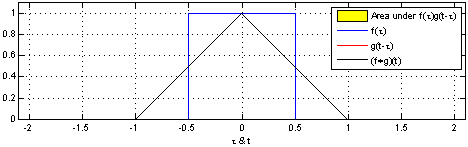
Tôi thấy trên hình vẽ này của wiki có chú thích phần màu vàng là diện tích dưới \(\mathbf{f(𝜏)g(t-𝜏)}\) không sai nhưng bản thân phần màu vàng lại trông như đang mô tả diện tích phần giao nhau giữa 2 hàm số. Nên các bạn cần phân biệt rõ, phần màu vàng là tổng của các f(𝜏)g(t-𝜏) không phải là diện tích phần giao nhau. Đến đây hi vọng các bạn đã mù mờ về convolution (tích chập) là gì, trong bài viết sau ta sẽ cùng nhau tìm hiểu xem convolution trong ML hay mạng neural. Hẹn gặp lại các bạn trong bài viết sau.
